Cho hai hàm số $\Large y=\ln \left| \dfrac{x-1}{x+1} \right|$ và $\Lar

Cho hai hàm số $\Large y=\ln \left| \dfrac{x-1}{x+1} \right|$ và $\Large y=\dfrac{3}{x-1}-\dfrac{1}{x+1}+8m-2021$. Gọi $\Large S$là tập tất cả các giá trị của $\Large m$để đồ thị 2 hàm số đã cho có đúng một điểm chung. Số phần tử của $\Large S$là

• A. $\Large 2021$.
• B. $\Large 2020$.
• C. $\Large 2$.
• D. $\Large 3$.

Chọn B
Điều kiện ban đầu: $\Large x\ne \pm 1$
Phương trình hoành độ giao điểm của 2 đồ thị hàm số trên tương đương với
$\Large \Rightarrow \ln \left| \dfrac{x-1}{x+1} \right|=\dfrac{3}{x-1}-\dfrac{1}{x+1}+8m-2021\Leftrightarrow 8m$$\Large =\ln \left| \dfrac{x-1}{x+1} \right|-\dfrac{3}{x-1}+\dfrac{1}{x+1}+2021$ (*)
Ta xét hàm $\Large y=g(x)=\ln \left| \dfrac{x-1}{x+1} \right|-\dfrac{3}{x-1}+\dfrac{1}{x+1}+2021$ có $\Large g'(x)=\dfrac{1}{x-1}-\dfrac{1}{x+1}-\dfrac{1}{{{\left( x+1 \right)}^{2}}}+\dfrac{3}{{{\left( x-1 \right)}^{2}}}$. Cho $\Large g'(x)=0\Leftrightarrow \dfrac{4{{x}^{2}}+8x}{{{\left( x-1 \right)}^{2}}{{\left( x+1 \right)}^{2}}}=0\Leftrightarrow \left[ \begin{matrix}
& x=-2 \\ 
& x=0 \\ 
\end{matrix} \right.$
$\Large \underset{x\to +\infty }{\mathop{\lim }}\,g(x)=\underset{x\to -\infty }{\mathop{\lim }}\,$$\Large g(x)=2021;f(-2)=2021+\ln 3,f(0)=2025$

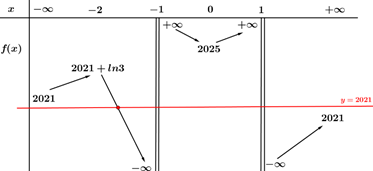
Như vậy, ta có bảng biến thiên của hàm $\Large g(x)$ như sau: 
Vậy, dựa vào BBT phía trên, để đồ thị 2 hàm số đã cho có đúng một điểm chung thì tương đương
với phương trình (*) có 1 nghiệm duy nhất
$\Large \Leftrightarrow \left[ \begin{matrix}
& 8m=2025 \\ 
& 8m=2021 \\ 
& 8m=2021+\ln 3 \\ 
\end{matrix} \right.\Leftrightarrow \left[ \begin{matrix}
& m=\dfrac{2025}{8} \\ 
& m=\dfrac{2021}{8} \\ 
& m=\dfrac{2021+\ln 3}{8} \\ 
\end{matrix} \right.$.
Như vậy có tất cả 3 giá trị m thỏa mãn yêu cầu đề bài.