Trong không gian $\Large Oxyz,$ cho hai điểm $\Large A(4;-2;4)$, $\Lar

Trong không gian  $\Large Oxyz,$ cho hai điểm $\Large A(4;-2;4)$, $\Large B(-2;6;4)$ và đường thẳng $\Large d:\left\{ \begin{matrix}
  & x=5 \\ 
 & y=-1 \\ 
 & z=t \\ 
\end{matrix} \right..$Gọi M là điểm di động thuộc mặt phẳng  $\Large \left( Oxy \right)$ sao cho  $\Large \widehat{AMB}={{90}^{\text{o}}}$ và N là điểm di động thuộc $\Large d.$ Tìm giá trị nhỏ nhất của $\Large MN.$

• A. 2
• B. $\Large 8$.
• C. $\Large \sqrt{73}$.
• D. $\Large 5\sqrt{3}$.

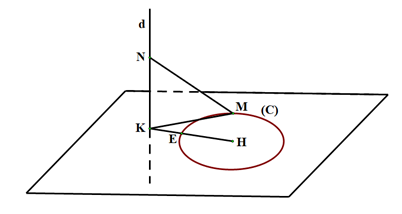
$\Large \widehat{AMB}={{90}^{\text{o}}}$ nên $\Large M$thuộc mặt cầu đường kính  $\Large AB$, có tâm  $\Large I\left( 1;2;4 \right);R=\dfrac{AB}{2}=5$. Mặt khác $\Large M$là điểm di động thuộc mặt phẳng  $\Large \left( Oxy \right)$ nên $\Large M$thuộc đường tròn  $\Large \left( C \right)$ là giao của mặt cầu với mặt phẳng  $\Large \left( Oxy \right).$ Đường tròn này có tâm  $\Large H\left( 1;2;0 \right)$ là hình chiếu của  $\Large I$ trên $\Large \left( Oxy \right).$ bán kính $\Large r=\sqrt{{{R}^{2}}-I{{H}^{2}}}=3$.
Gọi K là giao điểm của mặt phẳng  $\Large \left( Oxy \right)$và đường thẳng $\Large d:\left\{ \begin{matrix}
& x=5 \\ 
& y=-1 \\ 
& z=t \\ 
\end{matrix} \right..$

Suy ra  $\Large K\left( 5;-1;0 \right),HK=5$.
Nhận thấy $\Large d\bot \left( Oxy \right)$ tại  $\Large K$. Gọi  $\Large E=HK\cap \left( Oxy \right)$,  $\Large E$ nằm giữa  $\Large HK$,
Ta có  $\Large \forall M\in \left( C \right),N\in d:\,\,MN\ge MK\ge KE.$ Vậy  $\Large EK$là giá trị nhỏ nhất của $\Large MN.$
Lại có $\Large HE=r=3\Rightarrow KE=2$