Cho hình chóp $\Large {S.ABCD}$ có đáy $\Large {ABCD}$ là hình thang v

Cho hình chóp $\Large {S.ABCD}$ có đáy $\Large {ABCD}$ là hình thang vuông tại $\Large A$ và $\Large B$ .Biết $\Large {AB=BC=a,AD=2a,SA}$ vuông góc với đáy và $\Large {SA=2a.}$ Tính bán kính mặt cầu ngoại tiếp hình chóp $\Large {S.HCD}$ với $\Large H$ là trung điểm của $\Large {AD}$.

• A. $\Large \dfrac{a\sqrt{11}}{2}$.
• B. $\Large \dfrac{a\sqrt{10}}{2}$.
• C. $\Large \dfrac{a\sqrt{2}}{2}$.
• D. $\Large \dfrac{a\sqrt{3}}{2}$.

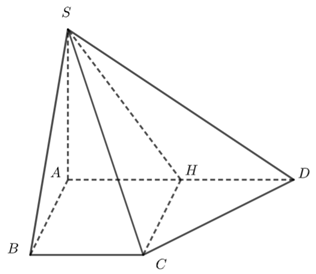
Ta có ABCH là hình vuông nên $\Large CH\bot AD\Rightarrow CH\bot \left( SAD \right).$
Lại có $\Large SA=AD=2a$ nên tam giác $\Large SAD$ vuông cân nên $\Large \widehat{SDA}={{45}^{0}}.$
Mà $\Large SH=\sqrt{S{{A}^{2}}+A{{H}^{2}}}\Rightarrow SH=a\sqrt{5}\Rightarrow {{R}_{\Delta SHD}}=\dfrac{SH}{2\sin \left( {{45}^{0}} \right)}=\dfrac{a\sqrt{10}}{2}.$
Hình chóp $\Large C.SHD$ có cạnh bên vuông góc với mặt đáy nên $\Large R=\sqrt{R_{\Delta SHD}^{2}+{{\left( \dfrac{CH}{2} \right)}^{2}}}=\dfrac{a\sqrt{11}}{2}$