Có bao nhiêu số nguyên m thỏa mãn $\Large \dfrac{\ln x}{x+1}+

MỤC LỤC
Câu hỏi:
Có bao nhiêu số nguyên m thỏa mãn lnxx+1+1x>lnxx−1+mx, ∀x>0, x≠1?
Đáp án án đúng là: C
Lời giải chi tiết:
Chọn C
Với x>0, x≠1 ta có:
lnxx+1+1x>lnxx−1+mx⇔mx<lnx(1x+1−1x−1)+1x⇔m<−2xlnxx2−1+1=f(x)
Xét hàm số: f(x)=−2xlnxx2−1+1 với x>0, x≠0.
Ta có: f′(x)=2.x2lnx+lnx+1−x2(x2−1)2.
f′(x)=0⇔x2lnx+lnx+1−x2=0 (1).
Xét hàm số g(x)=x2lnx+lnx+1−x2 với x>0
Đạo hàm g′(x)=2xlnx+1x−x
g″(x)=2lnx+1−1x2.
g‴(x)=2x+1x3>0, ∀x>0 ⇒\Large Hàm số g″(x) đồng biến trên khoảng (0;+∞).
Từ đó suy ra phương trình g″(x)=0 nếu có nghiệm thì nghiệm đó là duy nhất.
Lại có g″(1)=0. Suy ra phương trình g″(x)=0 có nghiệm duy nhất x=1.
Bảng biến thiên của hàm số y=g′(x):
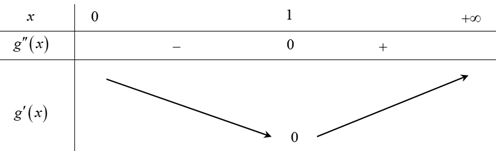
Từ bảng biến thiên suy ra phương trình g′(x)=0 có nghiệm duy nhất x=1.
Bảng biến thiên của hàm số y=g(x):
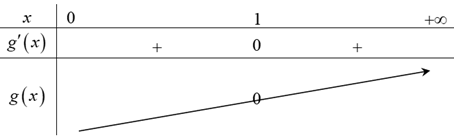
Từ bảng biến thiên suy ra phương trình g(x)=0 có nghiệm duy nhất x=1.
Giới hạn:
lim.
Bảng biến thiên của hàm số \Large y=f\left( x \right):
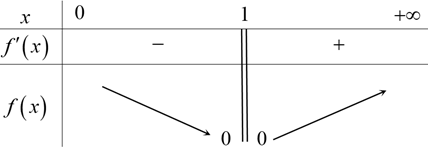
Bất phương trình $\Large m
Xem thêm các bài tiếp theo bên dưới
- Trong không gian \Large Oxyz, cho hai điểm \Large A(4;-2;4), $\Lar
- Cho hai hàm số \Large y=\ln \left| \dfrac{x-1}{x+1} \right| và $\Lar
- Mệnh đề nào sau đây sai? $\Large \int\dfrac{1}{2x+1}dx=\dfrac{1}{2}\ln
- Cho biểu thức \Large P=\sqrt[4]{x^{5}}, với \Large x > 0. Mệnh đề
- Trong không gian Oxyz, cho hai điểm A(3;-4;3) và B(-1;2;5). Tìm tọa độ