Cho tứ diện đều cạnh a, điểm I nằm trong tứ diện. Tính tổng khoảng các

Cho tứ diện đều cạnh a, điểm I nằm trong tứ diện. Tính tổng khoảng cách từ I đến tất cả các mặt của tứ diện

• A. A. $\large \dfrac{a\sqrt{6}}{3}$
• B. B. $\large \dfrac{a}{\sqrt{2}}$
• C. C. $\large \dfrac{a\sqrt{3}}{2}$
• D. D. $\large \dfrac{a\sqrt{34}}{3}$

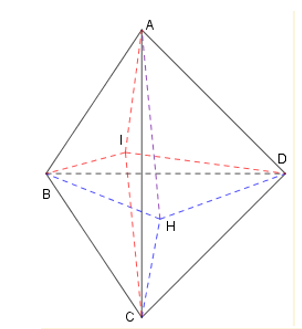
Giả sử ABCD là tứ diện đều và I là một điểm trong tứ diện. Gọi H là trọng tâm của tam giác BCD. Do ABCD là tứ diện đều nên AH là đường cao của tứ diện. Theo giả thiết và theo công thức tính thể tích của tứ diện ta có: 
$\large V_{ABCD}= V_{IABC}+V_{IABD}+V_{IBCD}+ V_{IACD}$
$\large = \dfrac{1}{3}.d(I, (ABC)).S_{ABC}+ \dfrac{1}{3}.d(I, (ABD)).S_{ABD}+ \dfrac{1}{3}d(I, BCD)).S_{BCD}+ \dfrac{1}{3}.d(I, (ACD)).S_{ACD}$
$\large \dfrac{1}{3}. \left[ d(I, (ABC))+ d(I, (ABD))+ d(I, (BCD))+ d(I, (ACD))\right]. S_{BCD}$
Mặt khác ta lại có: $\large V_{ABCD}= \dfrac{1}{3}AH. S_{BCD}$. Do đó tổng khoảng cách $\large d= AH$. Kéo theo $\large d= AH= \sqrt{AB^2- BH^2}= \sqrt{a-\left( \dfrac{a}{\sqrt{3}}\right)^2}= \dfrac{a\sqrt{6}}{3}$