Cho tứ diện ABCD, gọi M, N lần lượt là trung điểm của BC và AD. Biết $

Cho tứ diện ABCD, gọi M, N lần lượt là trung điểm của BC và AD. Biết $\large AB= CD= a,\, MN= \dfrac{a\sqrt{3}}{2}$. Tính góc giữa hai đường thẳng AB và CD

• A. A. $\large 45^\circ $
• B. B. $\large 30^\circ $
• C. C. $\large 60^\circ $
• D. D. $\large 90^\circ $

Chọn C

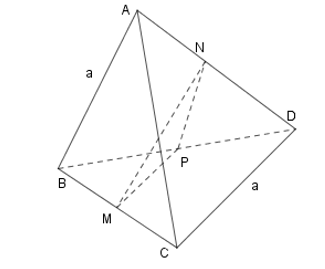
Gọi P là trung điểm của BD. Khi đó: M, N lần lượt là trung điểm của BC và AD nên ta có: $\large MP // = \dfrac{1}{2}CD= \dfrac{a}{2};\, NP// = \dfrac{1}{2}AB= \dfrac{a}{2}$
Do đó: $\large \widehat{(AB, CD)} = \widehat{(MP, NP)}$
Áp dụng định lý cosin trong tam giác MPN ta có: 
$\large \cos\widehat{MPN}= \dfrac{MP^2+NP^2-MN^2}{2MP.NP}= \dfrac{\left( \dfrac{a}{2}\right)^2+ \left( \dfrac{a}{2}\right)^2 - \left( \dfrac{a\sqrt{3}}{2}\right)^2}{2. \dfrac{a}{2}. \dfrac{a}{2}}$
Kéo theo $\large \widehat{(MP, NP)}= 180^\circ – 120^\circ = 60^\circ $
Vì vậy $\large \widehat{(AB, CD)}= 60^\circ $