Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, $\large SA=a$ v

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, $\large SA=a$ và vuông góc với mặt đáy (ABCD). Khoảng cách giữa hai đường thẳng SC và BD bằng: 

• A. A. $\large \dfrac{a\sqrt{3}}{4}$
• B. B. $\large \dfrac{a\sqrt{6}}{3}$
• C. C. $\large \dfrac{a}{2}$
• D. D. $\large \dfrac{a\sqrt{6}}{6}$

Chọn D

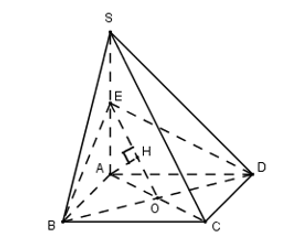
Gọi E là trung điểm của SA và O là tâm hình vuông ABCD
Ta có: $\large OE//SC\Rightarrow SC//(EBD)\Rightarrow d(SC, BD)= d(SC, (EBD))= d(C, (EBD))$
Ta có: $\large CA\cap (EBD)= O\Rightarrow \dfrac{d(C, (EBD))}{d(A, (EBD))}= \dfrac{CO}{AO}= 1\Rightarrow d(C, (EBD))= d(A, (EBD))$
Trong (SAC) kẻ $\large AH\perp OE$ (1)
Ta có: $\large \left\{\begin{align}& BD\perp AC\\& BD\perp SA\\\end{align} \right.$ $\large \Rightarrow BD\perp (SAC)\Rightarrow BD\perp AH$ (2)
Từ (1) và (2) $\large \Rightarrow AH\perp (EBD)\Rightarrow d(A, (EBD))= AH$
ABCD là hình vuông cạnh a $\large \Rightarrow AC= a\sqrt{2}\Rightarrow AO= \dfrac{a\sqrt{2}}{2},\, AE= \dfrac{1}{2}SA= \dfrac{a}{2}$
Ta có: $\large \dfrac{1}{AH^2}= \dfrac{1}{SE^2}+ \dfrac{1}{AO^2}= \dfrac{4}{a^2}+ \dfrac{2}{a^2}= \dfrac{6}{a^2}\Rightarrow AH= \dfrac{a\sqrt{6}}{6}= d(SC, BD)$