Hình chóp đều S. ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Gọi H là t

Hình chóp đều S. ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Gọi H là trung điểm của BC, khoảng cách từ S đến AH bằng 

• A. A. $\large 2a$
• B. B. $\large $a\sqrt{3}
• C. C. $\large a$
• D. D. $\large a\sqrt{5}$

Chọn C

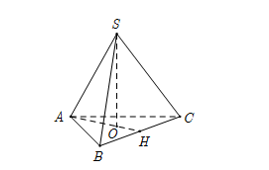
Gọi O là chân đường cao của hình chóp nên O là tam giác đáy
Go đó: O là trọng tâm tam giác ABC hay $\large O\in AH$
Ta có: $\large AO=\dfrac{2}{3}AH=\dfrac{2}{3}.3a.\df{\sqrt{3}}{2}=a\sqrt{3}$
$\large d(S, AH)= SO=\sqrt{SA^2-AO^2}= a$