Cho hình chóp tứ giác đều có cạnh đáy bằng a và chiều cao bằng $\large

Cho hình chóp tứ giác đều có cạnh đáy bằng a và chiều cao bằng $\large \dfrac{a\sqrt{3}}{2}$. Tính số đo góc giữa mặt bên và mặt đáy

• A. A. $\large 45^\circ $
• B. A. $\large 75^\circ $
• C. C. $\large 30^\circ $
• D. D. $\large 60^\circ $

Chọn D

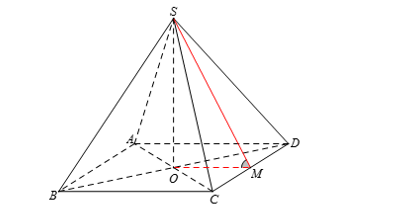
Gọi O là tâm hình vuông ABCD, M là trung điểm của CD
$\large \left\{\begin{align}&(SCD)\cap (ABCD)=CD\\& SM\subset (SCD):\, SM\perp CD\\& MO\subset (ABCD):\, OM\perp CD \\\end{align} \right.$ $\large \Rightarrow  \angle ((SCD),(ABCD))= \angle (SM, OM)= \widehat{SMO}$
$\large \tna\widehat{SMO}= \dfrac{SO}{OM}= \dfrac{\dfrac{a\sqrt{3}}{2}}{\dfrac{a}{2}}= \sqrt{3}\Rightarrow  \widehat{SMO}= 60^\circ $