Cho hình chóp S.ABCD có đáy ABCD là hình thoi. Biết rằng tứ diện SABD

Cho hình chóp S.ABCD có đáy ABCD là hình thoi. Biết rằng tứ diện SABD là tứ diện đều cạnh a. Khoảng cách giữa hai đường thẳng BD và SC bằng: 

• A. A. $\large \dfrac{3a\sqrt{3}}{4}$
• B. B. $\large \dfrac{a}{2}$
• C. C. $\large \dfrac{a\sqrt{3}}{4}$
• D. D. $\large \dfrac{a\sqrt{3}}{2}$

Chọn B

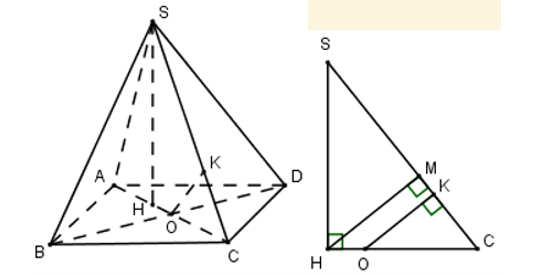
Gọi $\large O= AC\cap BD$, H là tâm của tam giác đều ABD, SABD là tứ diện đều
$\large \Rightarrow SH\perp (ABD)\Rightarrow SH\perp (ABCD)$
Ta có: $\large \left\{\begin{align}& BD\perp SH\, (SH\perp (ABCD))\\& BD\perp AC\\\end{align} \right.$ $\large \Rightarrow BD\perp (SAC)$
Trong (SAC) kẻ $\large OK\perp SC\, (K\in SC)\Rightarrow OK\perp BD$
Do đó: OK là đoạn vuông góc chung của BD và SC $\large \Rightarrow d(BD, SC)= OK$
Tam giác ABD đều cạnh a
$\large \Rightarrow AO= \dfrac{a\sqrt{3}}{2}\Rightarrow AH= \dfrac{2}{3}. \dfrac{a\sqrt{3}}{2}= \dfrac{a\sqrt{3}}{3}\Rightarrow SH = \sqrt{SA^2- AH^2}= \dfrac{a^2- \left( \dfrac{a\sqrt{3}}{3}\right)^2}= \dfrac{a\sqrt{6}}{3}$
$\large AH= \dfrac{2}{3}AO = \dfrac{2}{3}. \dfrac{1}{3}AC\Rightarrow HC= \dfrac{2}{3}.2AO= \dfrac{4}{3}. \dfrac{a\sqrt{3}}{2}= \dfrac{2\sqrt{3}}{3}$
Trong tam giác vuông SHC kẻ $\large HM\perp SC\, (M\in SC)$, ta có: 
$\large HM= \sqrt{\dfrac{SH^2.HC^2}{SH^2+ HC^2}}= \sqrt{\dfrac{\left( \dfrac{a\sqrt{6}}{3}\right)^2. \left( \dfrac{2\sqrt{3}}{3}\right)^2}{\left( \dfrac{a\sqrt{6}}{3}\right)^2+ \left( \dfrac{2a\sqrt{3}}{3}\right)^2}}$
Ta có: $\large OH= \dfrac{1}{3}AO= \dfrac{1}{3}OC\Rightarrow \dfrac{CO}{CH}= \dfrac{3}{4}\Rightarrow \dfrac{OK}{HM}= \dfrac{CO}{CH}= \dfrac{3}{4}\Rightarrow OK= \dfrac{3}{4}HM= \dfrac{a}{2}$