Cho tứ diện đều ABCD cạnh a. Gọi K là trung điểm của AB, M, N lần lượt

Cho tứ diện đều ABCD cạnh a. Gọi K là trung điểm của AB, M, N lần lượt là hình chiếu của K lên AD và AC. Tính theo a bán kính mặt cầu ngoại tiếp hình chóp K.CDMN?

• A.

  A. $\large \dfrac{a\sqrt{3}}{4}$

• B.

  B. $\large \dfrac{3a\sqrt{3}}{8}$

• C.

  C. $\large \dfrac{a\sqrt{2}}{4}$

• D.

  D. $\large \dfrac{3a\sqrt{2}}{8}$

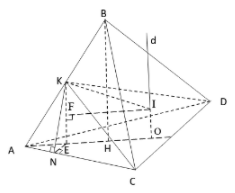
Tứ diện ABCD đều, có độ dài cạnh là a.

Gọi H là trọng tâm tam giác ACD khi đó $\large BH \perp (ACD)$. Gọi E là trung điểm của AH, suy ra $\large KE \perp (ACD)$. Từ E hạ EN vuông góc xuống AC, $\large N \in AC$, suy ra $\large KN \perp AC$ 

Gọi O là tâm đường tròn ngoại tiếp tam giác NCD. $\large O \in AH$ 

Ta tính được $\large ON = OC = OD = \dfrac{\sqrt{39}}{12}a$. Dựng đường thẳng d đi qua O, vuông góc với (ACD).

Gọi I là tâm mặt cầu ngoại tiếp chóp K.MNCD, $\large IF \perp KE = {F}$ ( Với IF là  đường trung trực của KE) suy ra OEFI là hình chữ nhật.

Ta tính được: $\large NE = \dfrac{1}{2}.\dfrac{1}{3}.\dfrac{\sqrt{3}}{2}a = \dfrac{\sqrt{3}}{12}a$;

$\large OE = \dfrac{\sqrt{3}}{4}a$; $\large KE = \dfrac{\sqrt{6}}{6}a$ 

Đặt OI = x ta có

$\large \begin{cases}
& \ IC^{2} = IO^{2}+OC^{2} = x^{2}+OC^{2}\\ 
& \ IK^{2} = IF^{2}+KF^{2} = OE^{2}+(KE-x)^{2}
\end{cases}$

Mà IC = IK nên 

$\large x^{2}+\dfrac{39}{144}a^2 = \dfrac{3}{16}a^2+\left (\dfrac{\sqrt{6}}{6}a-x  \right )^{2}$ 

suy ra $\large x = \dfrac{\sqrt{6}}{24}a$ 

Vậy $\large R_{mc} = IK = \dfrac{3\sqrt{2}}{8}a$