Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = a . C

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = a. Cạnh bên $\large SA = a\sqrt{2}$, hình chiếu của điểm S lên mặt phẳng đáy trùng với trung điểm của cạnh huyền AC. Bán kính mặt cầu ngoại tiếp khối chóp S.ABC là:

• A.

  A. $\large \dfrac{a\sqrt{2}}{2}$

• B.

  B. $\large \dfrac{a\sqrt{6}}{3}$

• C.

  C. $\large \dfrac{a\sqrt{6}}{2}$

• D.

  D. $\large \dfrac{a\sqrt{2}}{3}$

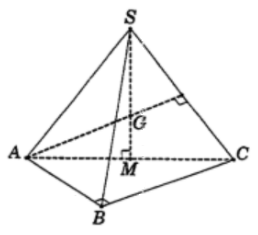
Gọi M là trung điểm AC, suy ra $\large SM \perp (ABC) \Rightarrow SM \perp AC$ 

Tam giác SAC có SM là đường cao và cũng là trung tuyến nên tam giác SAC cân tại S.

Ta có: $\large AC = AB^{2}+BC^{2} = a\sqrt{2}$, suy ra tam giác SAC đều.

Gọi G là trọng tâm $\large \Delta SAC$, suy ra GS = GA = GC.   (1)

Tam giác ABC vuông tại B, có M là trung điểm cạnh huyền AC nên M là tâm đường tròn ngoại tiếp tam giác ABC.

Lại có $\large SM \perp (ABC)$ nên SM là trục của tam giác ABC.

Mà G thuộc SM nên suy ra GA = GB = GC.   (2)

Từ (1) và (2), suy ra

 GS = GA = GB = GC hay G là tâm mặt cầu ngoại tiếp khối chóp S.ABC.

Bán kính mặt cầu $\large R = GS = \dfrac{2}{3}SM = \dfrac{a\sqrt{6}}{3}$. Chọn B.