Cho hình thang ABCD vuông tại A và D có CD = 2AB = 2AD = 4. Thể tích c

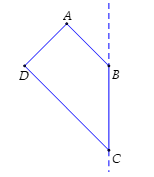
Cho hình thang ABCD vuông tại A và D có CD = 2AB = 2AD = 4. Thể tích của khối tròn xoay sinh ra bởi hình thang ABCD khi quay xung quanh đường thẳng BC bằng

• A. A. $\large \dfrac{28\sqrt{2}}{3}\pi$
• B. B. $\large \dfrac{20\sqrt{2}}{3}\pi$
• C. C. $\large \dfrac{32\sqrt{2}}{3}\pi$
• D. D. $\large \dfrac{10\sqrt{2}}{3}\pi$

Chọn A

Ta có: AB = AD = 2, $\large BD = \sqrt{AB^{2}+AD^{2}} = 2\sqrt{2}$;

$\large BC = \sqrt{AD^{2}+\left (\dfrac{1}{2}CD  \right )^{2}} = 2\sqrt{2}$.

Tam giác BCD vuông cân tại B do $\large CD^{2} = BD^{2}+BC^{2}$ và $\large BD = BC = 2\sqrt{2}$.

Kéo dài $\large AD\cap BC = E$. Kẻ $\large AF \perp BE$ tại F. Khi đó AF // BD. 

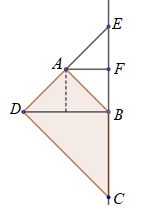
Dễ chứng minh: $\large \Delta BCD = \Delta BED$, $\large \Delta ABF = \Delta AEF$, $\large AF = BF = \dfrac{1}{2}BD = \sqrt{2}$ 

+Thể tích khối tròn xoay sinh ra bởi tam giác ECD khi quay xung quanh đường thẳng BC bằng 2 lần thể tích khối nón sinh ra bởi tam giác BCD khi quay xung quanh đường thẳng BC (bán kính đáy BD, đường cao BC):

$\large V_{1} = 2.\dfrac{1}{3}\pi BD^{2}.BC = \dfrac{32\sqrt{2}\pi }{3}$ 

+Thể tích khối tròn xoay sinh ra bởi tam giác ABE khi quay xung quanh đường thẳng BC bằng 2 lần thể tích khối nón sinh ra bởi tam giác ABF khi quay xung quanh đường thẳng BC (bán kính đáy AF, đường cao BF):

$\large V_{2} = 2.\dfrac{1}{3}\pi AF^{2}.BF = \dfrac{4\sqrt{2}}{3}\pi$ 

Thể tích khối tròn xoay sinh ra bởi hình thang ABCD khi quay xung quanh đường thẳng BC là:

$\large V = V_{1}-V_{2} = \dfrac{28\sqrt{2}}{3}\pi$.