Cho hình trụ có đáy là hai đường tròn tâm O và O ’, bán kính đáy bằng

Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính đáy bằng chiều cao và bằng 2a. Trên đường tròn đáy có tâm O lấy điểm A, D sao cho $\large  AD = 2\sqrt{3}$; gọi C là hình chiếu vuông góc của D lên mặt phẳng chứa đường tròn (O’); trên đường tròn tâm O’ lấy điểm B (AB chéo với CD). Đặt $\large \alpha$ là góc giữa AB và đáy. Tính $\large tan\alpha$ khi thể tích khối tứ diện CDAB đạt giá trị lớn nhất.

• A. A. $\large tan\alpha = \sqrt{3}$
• B. B. $\large tan\alpha = \dfrac{1}{\sqrt{2}}$
• C. C. $\large tan\alpha = 1$
• D. D. $\large tan\alpha = \dfrac{\sqrt{3}}{3}$

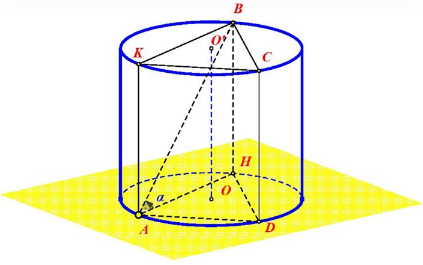
Gọi H là hình chiếu vuông góc của B lên mặt phẳng chứa đường tròn (O).

Gọi K là hình chiếu vuông góc của A lên mặt phẳng chứa đường tròn (O’).

Ta có HAD.BKC là một hình lăng trụ đứng.

Ta có thể tích của tứ diện CDAB là:

$\large V_{ABCD} = \dfrac{1}{3}V_{HAD.BKC} = \dfrac{1}{3}.2a.\dfrac{1}{2}.AD.d(H;AD) = \dfrac{1}{3}.2a.\dfrac{1}{2}.2a\sqrt{3}.d(H;AD)$.

$\large (V_{ABCD})_{max}\Leftrightarrow (d(H;AD))_{max}\Leftrightarrow$ H là điểm chính giữa cung lớn $\large \widehat{AD}$ của đường tròn (O).    (1)

Theo định lý sin ta có

$\large \dfrac{AD}{sin\widehat{AHD}} = 2.2a\Leftrightarrow sin\widehat{AHD} = \dfrac{AD}{4a} = \dfrac{2\sqrt{3}a}{4a} = \dfrac{\sqrt{3}}{2}$ 

nên $\large \widehat{AHD} = 60^{\circ}$ 

Do đó (1) xảy ra khi $\large \Delta AHD$ đều $\large \Leftrightarrow AH = AD = 2\sqrt{3}a$ 

Suy ra: $\large tan\alpha = tan\widehat{BAH} = \dfrac{BH}{AH} = \dfrac{2a}{2a\sqrt{3}} = \dfrac{\sqrt{3}}{3}$