Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C và BC = a. Mặt

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C và BC = a. Mặt phẳng (SAB) vuông góc với đáy, SA = SB = a, $\large \widehat{ASB} =120^{\circ}$. Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là:

• A.

  A. $\large \dfrac{a}{4}$

• B.

  B. $\large \dfrac{a}{2}$

• C.

  C. a

• D.

  D. 2a

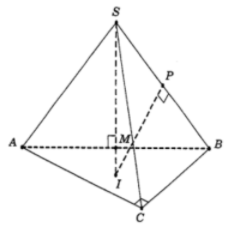
Gọi M là trung điểm AB, suy ra $\large SM \perp AB$ và $\large SM \perp (ABC)$.

Do đó SM là trục của tam giác ABC.

Trong mặt phẳng (SMB), kẻ đường trung trực d của đoạn SB cắt SM tại I. Khi đó I là tâm mặt cầu ngoại tiếp hình chóp S.ABC, bán kính R = SI.

Ta có $\large AB = \sqrt{SA^{2}+SB^{2}-2.SA.SB.cos\widehat{ASB}} = a\sqrt{3}$.

Trong tam giác vuông SMB, ta có 

$\large SM = SB.cos\widehat{MSB} = a.cos60^{\circ} = \dfrac{a}{2}$ 

Ta có $\large \Delta SMB\sim \Delta SPI$, suy ra

$\large \dfrac{SM}{SB} = \dfrac{SP}{SI} \Rightarrow R = SI = \dfrac{SB.SP}{SM} = a$ 

Chọn C.