Cho hai mặt phẳng ( P ) và ( Q ) song song với nhau và cắt một mặt cầu

MỤC LỤC
Câu hỏi:
Cho hai mặt phẳng (P) và (Q) song song với nhau và cắt một mặt cầu tâm O bán kính R tạo thành hai đường tròn có cùng bán kính. Xét hình nón có đỉnh trùng với tâm của một trong hai đường tròn và đáy trùng với đường tròn còn lại. Tính khoảng cách giữa (P) và (Q) để diện tích xung quanh hình nón đó là lớn nhất.
Đáp án án đúng là: D
Lời giải chi tiết:
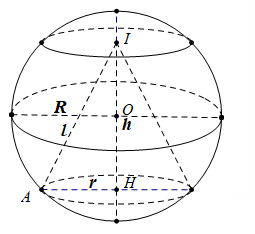
Chọn D.
Ta có $\large r = R^{2}-\dfrac{h^{2}}{4}, l = \sqrt{r^{2}+h^{2}} = \sqrt{R^{2}+\dfrac{3h^{2}}{4}}$
$\large S_{xq} = \pi rl = \pi \sqrt{R^{2}-\dfrac{h^{2}}{4}}\sqrt{R^{2}+\dfrac{3h^{2}}{4}}$
$\large = \pi \sqrt{-\dfrac{3}{16}h^{4}+\dfrac{R^{2}}{2}h^{2}+R^{4}}$
Xét $\large f(h) = -\dfrac{3}{16}h^{4}+\dfrac{R^{2}}{2}h^{2}+R^{4}$ (0
Ta có $\large f'(h) = -\dfrac{3}{4}h^{3}+R^{2}h, f'(h) = 0 \Leftrightarrow h = \dfrac{2R\sqrt{3}}{3}$
Bảng biến thiên:
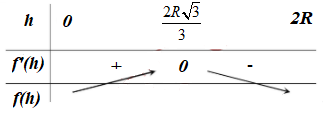
Khi đó f(h) đạt giá trị lớn nhất tại $\large h = \dfrac{2R\sqrt{3}}{3}$. Do đó $\large S_{xq}$ đạt giá trị lớn nhất khi $\large h = \dfrac{2R\sqrt{3}}{3}$.
Xem thêm các bài tiếp theo bên dưới
- Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = a . C
- Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a . Đường thẳ
- Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Mặt bên SAB là
- Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C và BC = a. Mặt
- Cho hình nón đỉnh S có đáy là đường tròn tâm O bán kính R . Trên đường