Cho tứ diện ABCD đều có cạnh bằng $\large 2\sqrt{2}$. Gọi G là trọng t

Cho tứ diện ABCD đều có cạnh bằng $\large 2\sqrt{2}$. Gọi G là trọng tâm tứ dinẹ ABCD và M là trung điểm của AB. Khoảng cách giữa hai đường thẳng BG và CM bằng

• A. A. $\large \dfrac{2}{\sqrt{14}}$
• B. B. $\large \dfrac{2}{\sqrt{5}}$
• C. C. $\large \dfrac{3}{2\sqrt{5}}$
• D. D. $\large \dfrac{2}{\sqrt{10}}$

Chọn B

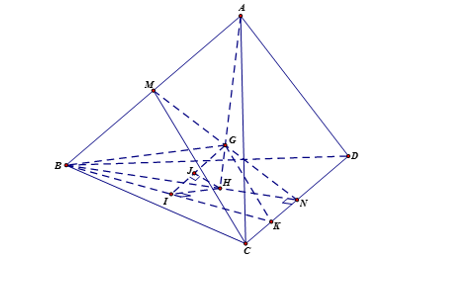
Gọi N là trung điểm của CD, khi đó G là trung điểm của MN và x đi qua trọng tâm H của tam giác BCD. Ta có: $\large AH\perp (BCD)$ và $\large AH=\sqrt{AB^2-BH^2}=\sqrt{\left( 2]\sqrt{2}\right)^2- \left( \dfrac{2\sqrt{6}}{3}\right)^2}= \dfrac{4\sqrt{3}}{3}$
Ta có: $\large GH= \dfrac{1}{4}AH= \dfrac{\sqrt{3}}{3}$
Gọi K là trung điểm của CN thì $\large GK// CM$ nên $\large CM// (BGK)$. Do đó: 
$\large d(BG, CM) = d(C, (BGK))= d(N, (BGK)) = \dfrac{3}{2}d(H, (BGK))$
Kẻ $\large HI\perp BK, HJ\perp GI$ với $\large I\in BK,\, J\in GI$. Khi đó: $\large HJ\perp (BGK)$ và $\large HJ= d(H, (BGK))$
Ta có: $\large BK=\sqrt{BN^2+NK^2}= \sqrt{\left( \sqrt{6}\right)^2+\left( \dfrac{\sqrt{2}}{2}\right)^2}=\dfrac{\sqrt{26}}{2}$
$\large HI= BH.\tan\widehat{KBN}= BH.\dfrac{KN}{BK}= \dfrac{2\sqrt{6}}{3}. \dfrac{\dfrac{\sqrt{2}}{2}}{\dfrac{\sqrt{26}}{2}}= \dfrac{2\sqrt{6}}{3\sqrt{13}}$
Do đó: $\large HJ= \dfrac{HI.HG}{\sqrt{HI^2+HG^2}}= \dfrac{\dfrac{2\sqrt{6}}{3\sqrt{13}}. \dfrac{\sqrt{3}}{3}}{\sqrt{\left( \dfrac{2\sqrt{6}}{3\sqrt{13}}\right)^2+\left( \dfrac{\sqrt{3}}{3}\right)^2}}$
Vậy $\large d(BG, CM)= \dfrac{3}{2}d(H, (BGK))= \dfrac{3}{2}HJ=\dfrac{3}{2}. \dfrac{2\sqrt{2}}{3\sqrt{7}}= \dfrac{2}{\sqrt{14}}$