Cho hình chóp S.ABC có SA vuông góc với đáy ABC. Tam giác ABC vuông câ

Cho hình chóp S.ABC có SA vuông góc với đáy ABC. Tam giác ABC vuông cân tại B và $\large SA= a\sqrt{2},\, SB= a\sqrt{5}$. Tính góc giữa SC và mặt phẳng (ABC)

• A. A. $\large 45^\circ $
• B. B. $\large 30^\circ $
• C. C. $\large 120^\circ $
• D. D. $\large 60^\circ $

Chọn B

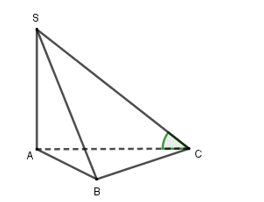
Vì $\large SA|\perp  (ABC)$ nên $\large \angle (SC, (ACB))= \angle (SC, AC)= \widehat{SCA}$ (vì $\large \widehat{SCA} < \widehat{A} = 90^\circ $)
Tam giác SAB vuông tại A có $\large SA= a\sqrt{2},\, SB= a\sqrt{5}\Rightarrow AB=\sqrt{SB^2- SA^2}= a\sqrt{3}\Rightarrow BC= a\sqrt{3}$
Do đó: $\large AC= \sqrt{AB^2+ BC^2}= \sqrt{3a^2+ 3a^2}= a\sqrt{6}$
Tam giác SAC vuông tại A có $\large \tan\widehat{SCA}= \dfrac{SA}{AC}= \dfrac{a\sqrt{2}}{a\sqrt{6}}= \dfrac{1}{\sqrt{3}}\Rightarrow \widehat{SCA}= 30^\circ $