Cho tứ diện ABCD có $\large BD= 2$, hai tam giác ABD, BCD có diện tích

Cho tứ diện ABCD có $\large BD= 2$, hai tam giác ABD, BCD có diện tích lần lượt là 6 và 10. Biết thể tích của tứ diện ABCD bằng 16, tính số đo góc giữa hai mặt phẳng (ABD) và (BCD)

• A. $\large arccos\left( \dfrac{4}{15}\right)$
• B. $\large arcsin\left( \dfrac{4}{15}\right)$
• C. $\large arcsin\left( \dfrac{4}{5}\right)$
• D. $\large arccos\left( \dfrac{4}{5}\right)$

Chọn C

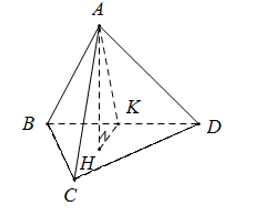
Vì $\large BD\perp AK,\, BD\perp AH\Rightarrow  BD\perp HK$
$\large \Rightarrow  $ Góc giữa (ABD) và (BCD) là góc giữa AK và HK và bằng $\large \widehat{AKH}$
$\large AH= \dfrac{3V_{ABCD}}{S_{BCD}}= \dfrac{3.16}{10}= \dfrac{24}{4};\, AK= \dfrac{2S_{ABD}}{BD}= \dfrac{2.6}{2}= 6$
$\large \sin \widehat{AKH}= \dfrac{AH}{AK} = \dfrac{4}{5}\Rightarrow  \qi{AKH} = arcsin \left(\dfrac{4}{5} \right)$