Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh bên SA vuông góc

Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh bên SA vuông góc với mặt phẳng  đáy. Đường thẳng SD tạo với mặt phẳng (SAB) một góc $\large 45^\circ $. Gọi I là trung điểm của cạnh CD. Góc giữa hai đường thẳng BI và SD bằng (làm tròn đến hàng đơn vị)

• A. $\large 39^\circ $
• B. $\large 42^\circ $
• C. $\large 51^\circ $
• D. $\large 48^\circ $

Chọn C

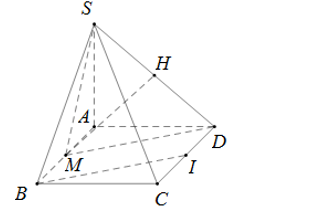
Gọi M là trung điểm của AB, ta có BMDI là hình bình hành $\large \Rightarrow MD//BI$
$\large $
Vì $\large DA\perp AB;\, DA\perp SA\Rightarrow  DA\perp (SAB)\Rightarrow  $ góc giữa SD và (SAB) là góc giữa SD và SA và bằng $\large $
$\large \Rightarrow  \Delta ASD$ vuông cân tại A
Gọi cạnh của hình vuông ABCD là a, ta có: 
$\large AM= \dfrac{AB}{2} = \dfrac{a}{2}$
$\large SM = \sqrt{SA^2+AM^2}= \dfrac{a^2+ \left( \dfrac{a}{2}\right)^2} = \dfrac{a\sqrt{5}}{2}$
$\large MD= \sqrt{AD^2+ AM^2} = \dfrac{a\sqrt{5}}}{2}$
$\large \Rightarrow  \Delta SMD$ cân tại M. Gọi H là trung điểm của SD $\large \Rightarrow  MH\perp SD$
$\large HD= SH = \dfrac{SD}{2} = \dfrac{\sqrt{SA^2+ AD^2}}{2} = \dfrac{a\sqrt{2}}{2}$
$\large \cos (SD, MD) = \cos\widehat{MDH}= \dfrac{HD}{MD} = \dfrac{\sqrt{2}}{\sqrt{5}} \Rightarrow  \angle{(SD, MD)}= arccps\dfrac{\sqrt{2}}{\sqrt{5}}\approx 51^\circ $