Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh A. Cạnh bên SA vuô

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh A. Cạnh bên SA vuông góc với đáy. Góc giữa SC và mặt phẳng đáy bằng $\large 45^\circ $. Gọi E là trung điểm của BC. Tính khoảng cách giữa hai đường thẳng DE và SC

• A. $\large \dfrac{a\sqrt{38}}{19}$
• B. $\large \dfrac{a\sqrt{38}}{5}$
• C. $\large \dfrac{a\sqrt{5}}{5}$
• D. $\large \dfrac{a\sqrt{5}}{19}$

Chọn A

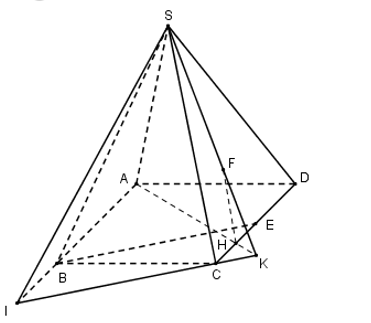
$\large SA|pw (ABCD)\Rightarrow  $ là hình chiếu của SC trên (ABCD) $\large \Rightarrow  \widehat{SCA}= 45^\circ $
$\large \Rightarrow  \Delta SAC$ vuông cân tại A $\large \Rightarrow  SA= AC= a\sqrt{2}$
Dựng $\large CI// DE$ suy ra $\large DE// (SIC)$
Dựng $\large AK\perp CI$ cắt DE tại H và cắt CI tại K
Trong (SAK) dựng $\large HF\perp SK$, do $\large CI\perp (SAK)$
$\large \Rightarrow  HF\perp (SCI),\, AK= \dfrac{BC.AI}{CI}= \dfrac{3a}{\sqrt{5}},\, HK= \dfrac{1}{3}AK= \dfrac{a}{\sqrt{5}}$
$\large SK= \sqrt{AK^2+ SA^2}= \dfrac{a\sqrt{95}}{5}$
$\large \Rightarrow  d(DE, SC)= d(H, (SCI))= HF= \dfrac{SA.HK}{SK}= \dfrac{a\sqrt{38}}{19} $