Cho hình hộp chữ nhật ABCD.A’B’C’D’ có các cạnh $\large AB= a,\, AD= 3

Cho hình hộp chữ nhật ABCD.A’B’C’D’ có các cạnh $\large AB= a,\, AD= 3,\, AA’= 4$. Góc giữa hai mặt phẳng (AB’D’) và (A’C’D) là $\large \alpha$. Tính giá trị gần đúng của góc $\large \alpha$?

• A. $\large 61,6^\circ$
• B. $\large 38,1^\circ$
• C. $\large 45,26\circ$
• D. $\large 53,4^\circ$

Chọn A

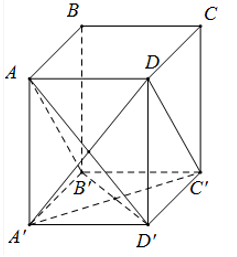
Xét hệ trục tọa độ Oxyz với $\large O\equiv A’,\, Ox\equiv A’D’,\, Oy\equiv A’A,\, Oz\equiv A’B’$
Tọa độ các điểm $\large D’(3; 0; 0),\, A(0; 4; 0),\, B’(0; 0; 2),\, D(3; 4; 0),\, C’(3; 0; 2)$
Phương trình mặt phẳng (AB’D’): $\large \dfrac{x}{3}+ \dfrac{y}{4}+ \dfrac{z}{2} = 1\Leftrightarrow 4a+ 3y+ 6z= 12\Rightarrow$ VTPT: $\large  \vec{n_1}= (4; 3; 6)$
Mặt phẳng (A’C’D) có VTPT:
$\large \vec{n_2}= \dfrac{1}{2} \left[ \overrightarrow{A’D}; \overrightarrow{A’C’}\right]= \dfrac{1}{2}(8; -6; -12) = (4; -3; -6)$
$\large \cos\alpha= \left| \cos\left( \overrightarrow{n_1}; \overrightarrow{n_2}\right)\right|= \dfrac{\left| 4.4-3.3-6.6\right|}{\sqrt{4^2+3^2+6^2}. \sqrt{4^2+ (-3)^2+ (-6)^2}}= \dfrac{29}{61}$
$\large \alpha = \arccos \dfrac{29}{61} \approx 61,6^\circ$