Cho hình chóp S.ABC có SA=SB=SCSA=SB=SC, góc $\large \widehat{ASB}

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABC có SA=SB=SCSA=SB=SC, góc ^ASB=90∘,^BSC=60∘,^ASC=120∘ˆASB=90∘,ˆBSC=60∘,ˆASC=120∘. Tính góc giữa đường thẳng SB và mặt phẳng (ABC)
Đáp án án đúng là: C
Lời giải chi tiết:
Chọn D
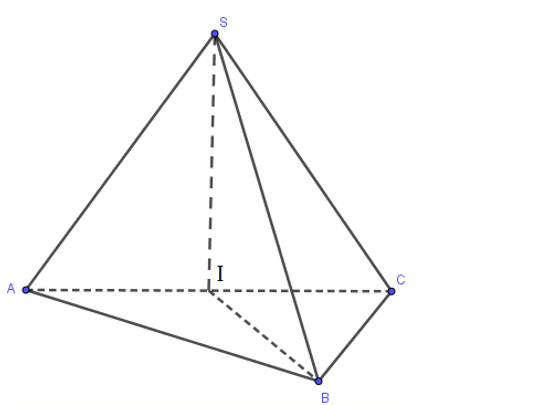
Đặt độ dài SA=SB=SC=aSA=SB=SC=a
ΔSABΔSAB vuông cân tại S, SA=SB=a⇒AB=√2SA=SB=a⇒AB=√2
ΔSBCΔSBC cân tại S có ^BSC=60∘⇒ΔSBCˆBSC=60∘⇒ΔSBC đều ⇒BC=SB=SC=a⇒BC=SB=SC=a
ΔSACΔSAC cân tại S có ^ASC=120∘ˆASC=120∘. Áp dụng định lý cosin, ta có:
AC=√SA2+SC2−2SA.SC.cos120∘=√a2+a2−2.a.\df−12=a√3AC=√SA2+SC2−2SA.SC.cos120∘=√a2+a2−2.a.\df−12=a√3
Xét ΔABCΔABC, ta thấy AB2+BC2=AC2AB2+BC2=AC2
⇒ΔABC⇒ΔABC vuông tại B
Do đó, tâm đường trong ngoại tiếp ΔABCΔABC là trung điểm của cạnh AC (ta gọi điểm đó là I)
Suy ra: SI⊥ABCSI⊥ABC
⇒BI⇒BI là hình chiếu của SB trên (ABC)
⇒∠(SB,(ABC))=∠(SB,IB)=^SBI⇒∠(SB,(ABC))=∠(SB,IB)=ˆSBI
Xét ΔABC:BI=AC2=a√32ΔABC:BI=AC2=a√32
Xét ΔSBIΔSBI có: \large \cos\widehat{SBI}= \dfrac{\dfrac{a\sqrt{3}}{2}}{a}= \dfrac{\sqrt{3}{2}\Rightarrow \widehat{SBI}= 30^\circ \Rightarrow \angle{(SB, (ABC))}= 30^\circ
Xem thêm các bài tiếp theo bên dưới
- Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh A. Cạnh bên SA vuô
- Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bằng 2. Đườ
- Hai cực nam châm khi đặt gần nhau chúng đẩy nhau thì có thể kết luận:
- Hồ quang điện được ứng dụng trong Hệ thống đánh lửa của động cơ. Lắp m
- Dòng điện trong chất khí là dòng chuyển dời có hướng của Các ion dương