Cho lăng trụ đứng ABC.A’B’C’ có $\large AB= AC= BB’= a,\, \widehat{BAC

Cho lăng trụ đứng ABC.A’B’C’ có $\large AB= AC= BB’= a,\, \widehat{BAC} 120^\circ $. Gọi I là trung điểm của CC’. Tính coisn của góc tạo bởi hai mặt phẳng (ABC) và (AB’I)

• A. $\large \dfrac{\sqrt{2}}{2}$
• B. $\large \dfrac{3\sqrt{2}}{12}$
• C. $\large \dfrac{\sqrt{30}}{10}$
• D. $\large \dfrac{\sqrt{3}}{2}$

Chọn C

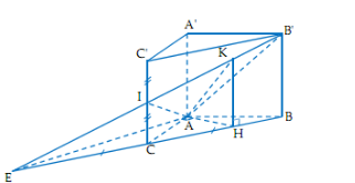
Gọi E là giao điểm của B’I và BC
$\large H\in BC$ sao cho $\large EA \perp AH$ tại A
$\large K\in B’I$ sao cho $\large KH\perp CB$ tại H
Có $\large KH\perp CB\Rightarrow  KH// CC’$
$\large \Rightarrow  KH\perp (ABC)$ tại H
$\large \Rightarrow  KH\perp EA$ mà $\large EA\perp AH\Rightarrow  EA\perp (AKH)\Rightarrow  EA\perp AK$
Hai mặt phẳng (AIB’) và (ACB) có giao tuyến là EA
Mà $\large AK\subcet (AIB’);\, AH\subset (ACB);\, EA\perp AK;\, Eape AH\Rightarrow  $ góc hợp bởi hai mặt phẳng (AIB’) và (ACB) là $\large \widehat{KAH}$
Ta có: $\large BC= 2a.\cos 30^\circ = a\sqrt{3}$
$\large AE^2= EC^2+ AC^2- 2.AC.EC.\cos \widehat{ACE}= 3a^2+ a^2- 2a.a\sqrt{3}. \cos 150^\circ = 7a^2\Rightarrow  AE= a\sqrt{7}$
Ta có: $\large \cos \widehat{AEC}= \dfrac{AE^2+ EC^2- AC^2}{2.AE.EC} = \dfrac{7a^2 + 3a^2- a^2}{2a\sqrt{7}.a\sqrt{3}}= \dfrac{9}{2\sqrt{21}}$
$\large \tan \widehat{AEC} = \sqrt{\dfrac{1}{\cos^2\widehat{AEC}}-1}= \dfrac{\sqrt{3}}{9}\Rightarrow  AH= AE. \tan \widehat{AEC}= \dfrac{a\sqrt{21}}9}$
Ta có: $\large \dfrac{EH}{EB}= \dfrac{HK}{BB’}\Rightarrow  HK= \dfrac{EH.BB’}{EB}= \dfrac{AE.BB’}{2.BC.\cos\widehat{AEC}}= \dfrac{a\sqrt{7}. 2\sqrt{21}}{2a\sqrt{3}. 9}= \dfrac{7a}{9}$
$\large \Rightarrow  \cos\widehat{KAH}= \dfrac{AH}{AK}= \dfrac{AH}{\sqrt{AH^2+ AK^2}}= \dfrac{a\sqrt{21}}{9. \sqrt{\dfrac{21a^2}{81} + \dfrac{42a^2}{81}}}= \dfrac{\sqrt{30}{10}$