Cho tứ diện ABCD có DA vuông góc với mp( ABC ), $\large DB \perp BC$ ,

MỤC LỤC
Câu hỏi:
Cho tứ diện ABCD có DA vuông góc với mp(ABC), $\large DB \perp BC$, AD = AB = BC = a. Kí hiệu $\large V_{1},V_{2},V_{3}$ lần lượt là thể tích của hình nón tròn xoay sinh bởi tam giác ABD khi quay quanh AD, tam giác ABC khi quay quanh AB, tam giác DBC khi quay quanh BC. Trong các mệnh đề sau, mệnh đề nào đúng?
Đáp án án đúng là: A
Lời giải chi tiết:
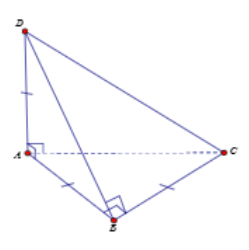
Chọn A
Quay tam giác ABD khi quay quanh AD ta có
$\large V_{1} = \dfrac{1}{3}AD.\pi .AB^{2} = \dfrac{\pi }{3}.a^{3}$ (đvtt)
Quay tam giác ABC khi quay quanh AB ta có
$\large V_{2} = \dfrac{1}{3}AB.\pi .BC^{2} = \dfrac{\pi }{3}.a^{3}$ (đvtt)
Quay tam giác DBC khi quay quanh BC ta có
$\large V_{3} = \dfrac{1}{3}BC.\pi .BD^{2} = \dfrac{\pi }{3}.AB.2AB^{2} = \dfrac{2\pi }{3}a^{3}$ (đvtt)
Vậy $\large V_{1}+V_{2} = V_{3}$
Xem thêm các bài tiếp theo bên dưới
- Thể tích V của khối tròn xoay thu được khi quay hình thang ABCD quanh
- Cho nửa đường tròn đường kính AB = 2R và điểm C thay đổi trên nửa đườn
- Cho một hình trụ có bán kính đáy R = 5, chiều cao h = 6. Một đoạn thẳn
- Cho hình trụ có đáy là hai đường tròn tâm O và O’ , bán kính đáy bằng
- Cho hình nón có độ dài đường kính đáy là 2 R , độ dài đường sinh là $\