Cho hình trụ có đáy là hai đường tròn tâm O và O’ , bán kính đáy bằng
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính đáy bằng chiều cao và bằng 2a. Trên đường tròn đáy có tâm O lấy điểm A, trên đường tròn tâm O’ lấy điểm B. Đặt α là góc giữa AB và đáy. Tính tanα khi thể tích khối tứ diện OO'AB đạt giá trị lớn nhất.
Đáp án án đúng là: B
Lời giải chi tiết:
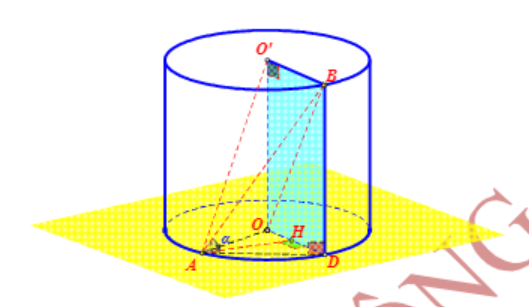
Gọi D là hình chiếu vuông góc của B lên mặt phẳng (O).
Kẻ AH⊥OD,H∈OD
Ta có thể tích của khối chóp OO'AB:
VOO′AB=13AH.SΔOO′B=2a23.AH≤2a23.AO=4a33
(VOO′AB)max⇔h≡O. Suy ra AD=2√2a
Suy ra: tanα=tan^BAD=1√2
Xem thêm các bài tiếp theo bên dưới
- Cho hình nón có độ dài đường kính đáy là 2 R , độ dài đường sinh là $\
- Một hình nón có tỉ lệ giữa đường sinh và bán kính đáy bằng 2. Góc ở đỉ
- Tính thể tích V của khối trụ có bán kính R = 4 và chiều cao $\large h
- Trong không gian cho tam giác ABC vuông tại A, AB = a và $\large \wide
- Cho hình nón có bán kính đáy là 4 a , chiều cao là 3 a . Diện tích xun