Cho hình nón có độ dài đường kính đáy là 2 R , độ dài đường sinh là $\
Lưu về Facebook:
MỤC LỤC
Câu hỏi:
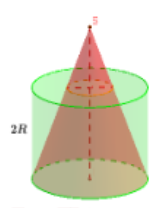
Cho hình nón có độ dài đường kính đáy là 2R, độ dài đường sinh là R√17 và hình trụ có chiều cao và đường kính đáy đều bằng 2R, lồng vào nhau như hình vẽ.

Tính thể tích phần khối trụ không giao với khối nón.
Đáp án án đúng là: D
Lời giải chi tiết:
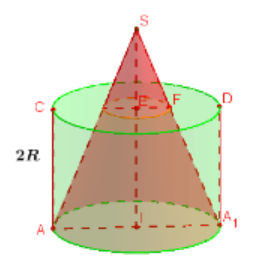
Ta có:
SI=√SB2−IB2=√17R2−R2=4R⇒SE=2R,EF=R2
Thể tích khối nón lớn (có đường cao SI) là
V1=13πR2.4R=43πR3
Thể tích khối nón nhỏ (có đường cao SE) là
V2=13π(R2)2.2R=16πR3
Thể tích phần khối giao nhau giữa khối nón và khối trụ là:
V3=V1−V2=V3=V1−V2=76πR3
Thể tích khối trụ là V4=πR2.2R=2πR3
Vậy thể tích phần khối trụ không giao với khối nón là V=V4−V3=56πR3
Xem thêm các bài tiếp theo bên dưới
- Một hình nón có tỉ lệ giữa đường sinh và bán kính đáy bằng 2. Góc ở đỉ
- Tính thể tích V của khối trụ có bán kính R = 4 và chiều cao $\large h
- Trong không gian cho tam giác ABC vuông tại A, AB = a và $\large \wide
- Cho hình nón có bán kính đáy là 4 a , chiều cao là 3 a . Diện tích xun
- Cho hình nón có đường sinh l , góc giữa đường sinh và mặt phẳng đáy là