Cho một hình trụ có bán kính đáy R = 5, chiều cao h = 6. Một đoạn thẳn

MỤC LỤC
Câu hỏi:
Cho một hình trụ có bán kính đáy R = 5, chiều cao h = 6. Một đoạn thẳng AB có độ dài bằng 10 và có hai đầu mút nằm trên hai đường tròn đáy. Tính khoảng cách giữa đường thẳng AB và trục của hình trụ?
Đáp án án đúng là: B
Lời giải chi tiết:
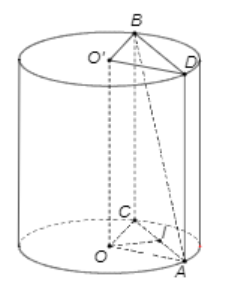
Gọi hai đường tròn đáy là (O), (O’) và $\large A \in (O), B \in (O)$. Kẻ hai đường sinh AD, BC ta được tứ giác ABCD là một hình chữ nhật và mp(ABCD) // OO’.
Do đó, khoảng cách giữa OO’ và AB bằng khoảng cách từ O đến mp(ABCD).
Tam giác ACB vuông tại C nên ta có:
$\large AC = \sqrt{AB^{2}-BC^{2}} = \sqrt{10^{2}-6^{2}} = 8$
Gọi I là trung điểm AC, ta có:
$\large \left\{\begin{matrix}
OI \perp AC & \\
OI \perp AD &
\end{matrix}\right.\Rightarrow OI \perp (ABCD)$
Vậy khoảng cách giữa đường thẳng AB và trục OO’ của hình trụ là:
$\large OI = \sqrt{OA^{2}-IA^{2}} = \sqrt{5^{2}-4^{2}} = 3$
Chọn B
Xem thêm các bài tiếp theo bên dưới
- Cho hình trụ có đáy là hai đường tròn tâm O và O’ , bán kính đáy bằng
- Cho hình nón có độ dài đường kính đáy là 2 R , độ dài đường sinh là $\
- Một hình nón có tỉ lệ giữa đường sinh và bán kính đáy bằng 2. Góc ở đỉ
- Tính thể tích V của khối trụ có bán kính R = 4 và chiều cao $\large h
- Trong không gian cho tam giác ABC vuông tại A, AB = a và $\large \wide