Cho tam giác $\Large ABC$ vuông tại $\Large A$, $\Large BC=a$, $\Large

Cho tam giác $\Large ABC$ vuông tại $\Large A$, $\Large BC=a$, $\Large AC=b$, $\Large AB=c$, $\Large b

• A. $\Large {{S}_{b}}>{{S}_{c}}>{{S}_{a}}$.
• B. $\Large {{S}_{b}}>{{S}_{a}}>{{S}_{c}}$.
• C. $\Large {{S}_{c}}>{{S}_{a}}>{{S}_{b}}$.
• D. $\Large {{S}_{a}}>{{S}_{c}}>{{S}_{b}}$.

Chọn A
 
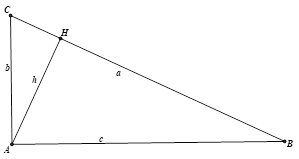
Gọi  $\Large H$ là hình chiếu của $\Large A$ lên cạnh  $\Large BC,AH=h$.
Khi quay tam giác vuông $\Large ABC$ một vòng quanh cạnh $\Large BC$ ta thu được hình hợp bởi hai hình nón tròn xoay có chung đáy bán kính bằng $\Large h$, đường sinh lần lượt là $\Large b,c$. Do đó $\Large {{S}_{a}}=\pi bh+\pi ch$.
Khi quay tam giác vuông $\Large ABC$ một vòng quanh cạnh $\Large AC$ ta thu được hình nón tròn xoay có bán kính đáy bằng $\Large c$, đường sinh bằng $\Large a$, $\Large {{S}_{b}}=\pi ac+\pi {{c}^{2}}=\pi c\left( a+c \right)$.
Khi quay tam giác vuông $\Large ABC$ một vòng quanh cạnh $\Large AB$ ta thu được hình nón tròn xoay có bán kính đáy bằng $\Large b$, đường sinh bằng $\Large a$, $\Large {{S}_{c}}=\pi ab+\pi {{b}^{2}}=\pi b\left( a+b \right)$.
Do $\Large b & ab & {{b}^{2}}<{{c}^{2}} \\ 
\end{matrix} \right.$$\Large \Rightarrow {{S}_{c}}<{{S}_{b}}$.
Ta có $\Large h=\dfrac{bc}{a}\Rightarrow {{S}_{a}}=\pi {{b}^{2}}.\dfrac{c}{a}+\pi {{c}^{2}}.\dfrac{b}{a}$.
Tam giác $\Large ABC$ vuông nên $\Large \dfrac{c}{a}<1\Rightarrow \pi {{b}^{2}}\dfrac{c}{a}<\pi {{b}^{2}}$; $\Large \dfrac{{{c}^{2}}}{{{a}^{2}}}<1\Rightarrow \pi {{c}^{2}}\dfrac{b}{a}<\pi ab$.
 $\Large \Rightarrow {{S}_{a}}<\pi {{b}^{2}}+\pi ab=\pi b\left( a+b \right)={{S}_{c}}$. Do đó $\Large {{S}_{a}}<{{S}_{c}}$.
Vậy  $\Large {{S}_{b}}>{{S}_{c}}>{{S}_{a}}$.