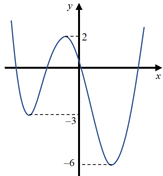
Cho hàm số $\Large y=f\left( x \right)$ là hàm đa thức bậc bốn có đồ t

Cho hàm số  $\Large y=f\left( x \right)$ là hàm đa thức bậc bốn có đồ thị như hình vẽ bên.

 
Có bao nhiêu giá trị nguyên của tham số  $\Large m$ thuộc đoạn  $\Large \left[ -12;12 \right]$ để hàm số  $\Large g\left( x \right)=\left| 2f\left( x-1 \right)+m \right|$ có 5 điểm cực trị?

• A. $\Large 13$.
• B. $\Large 14$.
• C. $\Large 15$.
• D. $\Large 12$.

Chọn C

Gọi  $\Large {{x}_{1}}$,  $\Large {{x}_{2}}$,  $\Large {{x}_{3}}$ là 3 điểm cực trị của hàm số  $\Large y=f\left( x \right)$ với  $\Large {{x}_{1}}<{{x}_{2}}<{{x}_{3}}$.

Hàm số  $\Large g\left( x \right)=\left| 2f\left( x-1 \right)+m \right|$ có 5 cực trị

 $\Large \Leftrightarrow 2f\left( x-1 \right)+m=0$ có hai nghiệm phân biệt khác  $\Large {{x}_{1}},{{x}_{2}},{{x}_{3}}$

 $\Large \Leftrightarrow f\left( x-1 \right)=-\dfrac{m}{2}$ có hai nghiệm phân biệt khác  $\Large {{x}_{1}},{{x}_{2}},{{x}_{3}}$

 $\Large \Leftrightarrow \left[ \begin{matrix}& -\dfrac{m}{2}\ge 2 \\ & -6<-\dfrac{m}{2}\le -3 \\ \end{matrix} \right.\Leftrightarrow \left[ \begin{matrix}& m\le -4 \\ & 6\le m<12 \\ \end{matrix} \right.$.

Vậy  $\Large m\in \left\{ -12;-11;...;-4;6;7;..;11 \right\}$.