Cho tam giác $\Large ABC$ đều có diện tích bằng $\Large S_1$ và đường

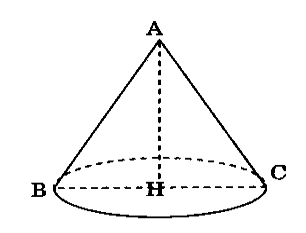
Cho tam giác $\Large ABC$ đều có diện tích bằng $\Large S_1$ và đường cao là $\Large AH$. Quay tam giác $\Large ABC$ quanh đường thẳng $\Large AH$ ta thu được hình nón có diện tích xung quang bằng $\Large S_2$. Tính tỉ số $\Large \dfrac{S_1}{S_2}$.

• A.

  $\Large \dfrac{2\sqrt{3}}{\pi}$.

• B.

  $\Large \dfrac{\sqrt{3}}{2\pi}$.

• C.

  $\Large \dfrac{\sqrt{3}}{\pi}$.

• D.

  $\Large \dfrac{4}{\sqrt{3}\pi}$.

Chọn B

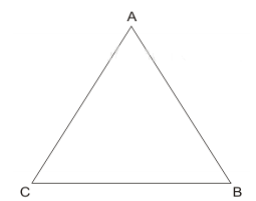
Gọi $\Large AB=a$ $\Large \Rightarrow$ diện tích tam giác $\Large ABC$ là $\Large S_1=\dfrac{a^2\sqrt{3}}{4}$.

Khi quay tam giác $\Large ABC$ quanh đường thẳng $\Large AH$ ta thu được hình nón có bán kính đường tròn đáy là $\Large r=\dfrac{1}{2}BC=\dfrac{a}{2}$ và có độ dài đường sinh $\Large l=AB=a$.

Diện tích xung quanh của hình nón $S_2=\pi rl=\dfrac{\pi a^2}{2}\Rightarrow \dfrac{S_1}{S_2}=\dfrac{\sqrt{3}}{2\pi}$