Cho tam giác $\Large ABC$ cân tại $\Large A$, có cạnh đáy $\Large BC$,

Cho tam giác $\Large ABC$ cân tại $\Large A$, có cạnh đáy $\Large BC$, đường cao $\Large AH$ và cạnh bên $\Large AB$ theo thứ tự lập thành một cấp số nhân có công bội là $\Large q$. Chọn mệnh đề đúng trong các mệnh đề sau.

• A.

  $\Large q\in (2; +\infty)$.

• B.

  $\Large q\in (0; 1)$.

• C.

  $\Large q\in \left(\dfrac{3}{2}; 2\right)$.

• D.

  $\Large q\in \left(1; \dfrac{3}{2}\right)$.

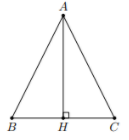
Đặt $\Large BC=x$ $\Large (x > 0)$. Do $\Large BC, AH, AB$ theo thứ tự lập thành một cấp số nhân với công bội là $\Large q$ nên $\Large AH=qx$, $\Large AB=q^2x$ và $\Large q > 0$.

Tam giác $\Large ABH$ vuông tại $\Large H$ nên 

$\Large AB^2=AH^2+BH^2$

$\Large \Leftrightarrow (q^2x)^2=(qx)^2+\left(\dfrac{x}{2}\right)^2$

$\Large \Leftrightarrow 4q^4-4q^2-1=0$

$\Large \Leftrightarrow q^2=\dfrac{1+\sqrt{2}}{2}$

$\Large \Leftrightarrow q=\sqrt{\dfrac{1+\sqrt{2}}{2}}\in \left(1; \dfrac{3}{2}\right)$.

Chọn đáp án D.