Cho số phức z thỏa mãn $\large |z-1| \leq 1$ và $\large z-\bar{z}$ có

Cho số phức z thỏa mãn $\large |z-1| \leq 1$ và $\large z-\bar{z}$ có phần ảo không âm. Tập hợp các điểm biểu diễn số phức z là một miền phẳng. Tính diện tích S của miền phẳng này

• A.

  A. $\large S=\pi$

• B.

  B. $\large S=2 \pi$

• C.

  C. $\large S=\dfrac{1}{2} \pi$

• D.

  D. 1

Chọn C

Đặt $\large z=x+y i(x, y \in \mathbb{R})$ theo giả thiết ta có $\large z-\bar{z}=(x+y i)-(x-y i)=2 y i$ và $\large \left\{\begin{array}{c}
|x+y i-1| \leq 1 \\
2 y \geq 0
\end{array} \Leftrightarrow\left\{\begin{array}{l}
(x-1)^{2}+y^{2} \leq 1 \\
y \geq 0
\end{array}\right.\right.$

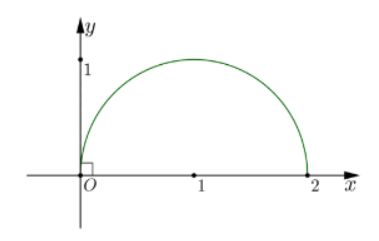
Vậy tập hợp các điểm biểu diễn số phức z là nửa hình tròn tâm I(1;0), R=1.

Vì vậy $\large S=\dfrac{\pi R^{2}}{2}=\frac{\pi}{2}$.