Cho số nguyên dương $\Large n$ và $\Large n$ tam giác $\Large A_1B_1C_

Cho số nguyên dương $\Large n$ và $\Large n$ tam giác $\Large A_1B_1C_1$, $\Large A_2B_2C_2$,..., $\Large A_nB_nC_n$, trong đó các điểm $\Large A_{i+1}$, $\Large B_{i+1}$, $\Large C_{i+1}$ lần lượt thuộc các đoạn thẳng $\Large B_iC_i$, $\Large C_iA_i$, $\Large A_iB_i$ với $\Large i=\overline{1,n-1}$ sao cho $\Large A_{i+1}C_i=2A_{i+1}B_i$, $\Large B_{i+1}A_i=2B_{i+1}C_i$, $\Large C_{i+1}B_i=2C_{i+1}A_i$. Gọi $\Large S$ là tổng tất cả diện tích của $\Large n$ tam giác đó. Tìm số nguyên dương $\Large n$ biết rằng $\Large S=3\left(1-\dfrac{2^{2018}}{3^{2018}}\right)$ và tam giác $\Large A_1B_1C_1$ có diện tích bằng 1.

• A.

  $\Large n=6054$.

• B.

  $\Large n=2027$.

• C.

  $\Large n=2017$.

• D.

  $\Large n=2018$.

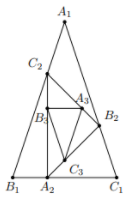
Gọi $\Large S_1, S_2,..., S_n$ lần lượt là diện tích các tam giác $\Large A_1B_1C_1$, $\Large A_2B_2C_2$,..., $\Large A_nB_nC_n$.

Ta có $\Large S_{B_1A_2C_2}=\dfrac{1}{2}B_1A_2.B_1C_2.sinB_1$ $\Large =\dfrac{1}{2}.\dfrac{1}{3}B_1C_1.\dfrac{2}{3}B_1A_1.sinB_1=\dfrac{1}{9}S_1$.

Tương tự $\Large S_{C_1B_2A_2}=S_{A_1C_2B_2}=\dfrac{1}{9}S_1$.

Suy ra $\Large S_2=S_1-3.\dfrac{1}{9}S_1=\dfrac{2}{3}S_1$. Chứng minh tương tự ta được $\Large S_n=\dfrac{2}{3}S_{n-1}$. 

Do đó dãy $\Large S_1, S_2,..., S_n$ là một cấp số nhân với $\Large S_1=1$ và công bội $\Large q=\dfrac{2}{3}$,

Suy ra $\Large S=\dfrac{1\left[1-\left(\dfrac{2}{3}\right)^n\right]}{1-\dfrac{2}{3}}=3\left(1-\dfrac{2^n}{3^n}\right)$.

Vậy $\Large n=2018$ thì thỏa mãn yêu cầu bài toán.

Chọn đáp án D.