Cho phương trình $\Large m\mathrm{ln}(x+1)-x-2=0$. Biết rằng tập hợp t

Cho phương trình $\Large m\mathrm{ln}(x+1)-x-2=0$. Biết rằng tập hợp tất cả các giá trị của tham số $\Large m$ để phương trình đã cho có hai nghiệm $\Large x_1, x_2$ thỏa mãn $\Large 0 < x_1 < 2 < 4 < x_2$ là khoảng $\Large (a; +\infty)$. Khi đó $\Large a$ thuộc khoảng nào dưới đây?

• A. $\large (3, 7;3, 8).$
• B. $\large (3, 6;3, 7).$
• C. $\large (3, 8; 3, 9).$
• D. $\large (3, 5; 3, 6).$

Chọn A

Xét trên khoảng $\Large (0; +\infty)$ phương trình: $\Large m\mathrm{ln}(x+1)-x-2=0$ $\Large \Leftrightarrow m=\dfrac{x+2}{\mathrm{ln}(x+1)}$

Đặt $\Large f(x)=\dfrac{x+2}{\mathrm{ln}(x+1)}$, $\Large x\in (-1; +\infty)\setminus \begin{Bmatrix} 0 \end{Bmatrix}$

Với yêu cầu của đề bài ta xét $\Large f(x)$ trên 2 khoảng $\Large (0; 2)$ và $\Large (4; +\infty)$

$\Large f'(x)=\dfrac{\mathrm{ln}(x+1)-(x+2)\dfrac{1}{x+1}}{\mathrm{ln}^2(x+1)}$

Đặt $\Large g(x)=\mathrm{ln}(x+1)-(x+2)\dfrac{1}{x+1}$, $\Large x\in (0; 2)\cup (4; +\infty)$

$\Large g'(x)=\dfrac{1}{x+1}+\dfrac{1}{(x+1)^2} > 0$, $\Large \forall x\in (0; 2)\cup (4; +\infty)$

Suy ra $\Large \left\{\begin{align} & g(x) < g(2)=\mathrm{ln}3-\dfrac{4}{3} < 0, \forall x\in (0; 2) \Rightarrow f'(x) < 0, \forall x\in (0; 2) \\ & g(x) > g(5)=\mathrm{ln}5-\dfrac{6}{5} > 0, \forall x\in (4; +\infty)\Rightarrow f'(x) > 0, \forall x\in (4; +\infty) \end{align}\right.$

Từ đó ta có bảng biến thiên

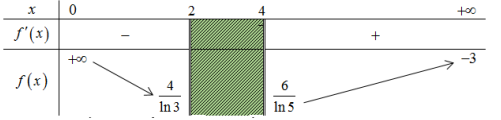
Dựa vào bảng biến thiên, để phương trình đề bài có 2 nghiệm phân biệt thỏa $\Large 0 < x_1 < 2 < 4 < x_2$ $\Large \Leftrightarrow m > \dfrac{6}{\mathrm{ln}5}(\approx 3,728)$.