Cho hình lăng trụ đứng $\Large ABC.A'B'C'$ có $\Large AA'=AB=AC=1$ và

Cho hình lăng trụ đứng $\Large ABC.A'B'C'$ có $\Large AA'=AB=AC=1$ và $\Large \widehat{BAC}=120^{\circ}$. Gọi $\Large I$ là trung điểm cạnh $\Large CC'$. Côsin góc giữa hai mặt phẳng $\Large (ABC)$ và $\Large (AB'I)$ bằng

• A.

  $\Large \dfrac{\sqrt{370}}{20}$.

• B.

  $\Large \dfrac{\sqrt{70}}{10}$.

• C.

  $\Large \dfrac{\sqrt{30}}{20}$.

• D.

  $\Large \dfrac{\sqrt{30}}{10}$.

Chọn D

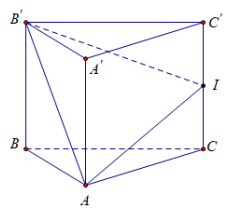
Gọi $\Large \varphi$ là góc giữa hai mặt phẳng $\Large (ABC)$ và $\Large (AB'I)$.

$\Large AB'=\sqrt{2}$, $\Large AI=\dfrac{\sqrt{5}}{2}$.

$\Large BC^2=AB^2+AC^2-2AB.AC.cos\widehat{A}=3$ $\Large \Rightarrow BC=B'C'=\sqrt{3}$.

$\Large B'I=\sqrt{B'C'^2+C'I^2}=\dfrac{\sqrt{13}}{2}$.

Vì $\Large AB'^2+AI^2=B'I^2$ $\Large \Rightarrow \Delta AB'I$ vuông tại điểm $\Large A$.

$\Large S_{ABC}=\dfrac{1}{2}AB.AC.sin\widehat{A}=\dfrac{\sqrt{3}}{4}$ và $\Large S_{AB'I}=\dfrac{1}{2}AI.AB'=\dfrac{\sqrt{10}}{4}$.

Hình chiếu vuông góc của $\Large \Delta AB'I$ lên mặt phẳng $\Large (ABC)$ là $\Large \Delta ABC$.

Ta có: $\Large S_{ABC}=S_{AB'I}.cos\varphi$ $\Large \Rightarrow cos\varphi =\dfrac{S_{ABC}}{S_{AB'I}}=\dfrac{\sqrt{30}}{10}$.