Cho hàm số $\Large f(x)=ax^3+bx^2+cx+d$ (với $\Large a, b, c, d\in \ma

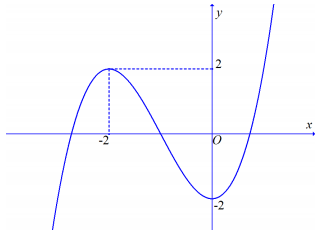
Cho hàm số $\Large f(x)=ax^3+bx^2+cx+d$ (với $\Large a, b, c, d\in \mathbb{R}$ và $\Large a\neq 0$) có đồ thị như hình vẽ. Số điểm cực trị của hàm số $\Large g(x)=f(-2x^2+4x)$

• A. 2.
• B. 5.
• C. 4.
• D. 3.

Chọn D
Dựa vào đồ thị hàm số $\Large y=f(x)$ có hai điểm cực trị là $\Large x=-2$; $\Large x=0$.

$\Large g(x)=f(-2x^2+4x)$ liên tục trên $\Large \mathbb{R}$. $\Large g'(x)=(-4x+4)f'(-2x^2+4x)$.

$\Large g'(x)=0$ $\Large \Leftrightarrow \left[\begin{align} & -4x+4=0 \\ & -2x^2+4x=0 \\ & -2x^2+4x=-2 \end{align}\right.$ $\Large \Leftrightarrow \left[\begin{align} & x=1 \\ & x=0 \\ & x=2 \\ & x=1\pm \sqrt{2} \end{align}\right.$

Như vậy $\Large g'(x)$ có 5 nghiệm đơn nên $\Large g(x)$ có 5 điểm cực trị.