Cho hình chóp $\Large S.ABC$ có đáy $\Large ABC$ là tam giác vuông cân

Cho hình chóp $\Large S.ABC$ có đáy $\Large ABC$ là tam giác vuông cân tại $\Large B$ và $\Large BC=a$. Cạnh bên $\Large SA$ vuông góc với đáy $\Large (ABC)$. Gọi $\Large H, K$ lần lượt là hình chiếu vuông góc của $\Large A$ lên $\Large SB$ và $\Large SC$. Thể tích của khối cầu ngoại tiếp hình chóp $\Large A.HKCB$ bằng

• A.

  $\Large \sqrt{2}\pi a^3$.

• B.

  $\Large \dfrac{\sqrt{2}\pi a^3}{3}$.

• C.

  $\Large \dfrac{\pi a^3}{6}$.

• D.

  $\Large \dfrac{\pi a^3}{2}$.

Chọn B

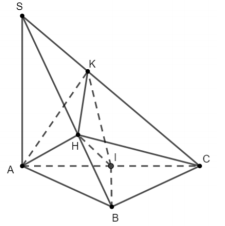
Gọi $\Large I$ là trung điểm của $\Large AC$. Do tam giác $\Large ABC$ vuông cân tại $\Large B$ nên $\Large IA=IB=IC=\dfrac{1}{2}AC$.

Do $\Large AK\perp SC$ nên $\Large \Delta AKC$ vuông tại $\Large K$, khi đó $\Large IA=IK=IC=\dfrac{1}{2}AC$.

Ta có $\Large BC\perp AB$, $\Large BC\perp SA$ $\Large \Rightarrow BC\perp (SAB)$ $\Large \Rightarrow BC\perp AH$, mà $\Large AH\perp SB$ nên $\Large AH\perp (SBC)$

$\Large \Rightarrow AH\perp HC$ hay $\Large \Delta AHC$ vuông tại $\Large H\Rightarrow IH=IA=IC=\dfrac{1}{2}AC$.

Như vậy $\Large IA=IB=IC=IH=\dfrac{1}{2}AC$ hay mặt cầu ngoại tiếp hình chóp $\Large A.HKCB$ có tâm $\Large I$ là trung điểm $\Large AC$, bán kính $\Large R=\dfrac{1}{2}AC=\dfrac{1}{2}.BC\sqrt{2}=\dfrac{a\sqrt{2}}{2}$.

Vậy thể tích khối cầu là $\Large V=\dfrac{4}{3}\pi R^3=\dfrac{4}{3}\pi \left(\dfrac{a\sqrt{2}}{2}\right)^3=\dfrac{\sqrt{2}\pi a^3}{3}$.