Cho hình vuông $\Large ABCD$ cạnh $\Large a$. Trên đường thẳng vuông g

Cho hình vuông $\Large ABCD$ cạnh $\Large a$. Trên đường thẳng vuông góc với $\Large (ABCD)$ tại $\Large A$ lấy điểm $\Large S$ di động không trùng với $\Large A$. Hình chiếu vuông góc của $\Large A$ lên $\Large SB, SD$ lần lượt tại $\Large H, K$. Tìm giá trị lớn nhất của thể tích khối tứ diện $\Large ACHK$.

• A.

  $\Large \dfrac{a^3\sqrt{6}}{32}$.

• B.

  $\Large \dfrac{a^3}{6}$.

• C.

  $\Large \dfrac{a^3\sqrt{3}}{16}$.

• D.

  $\Large \dfrac{a^3\sqrt{2}}{12}$.

Chọn C
 

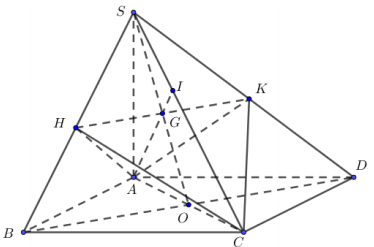
Đặt $\Large SA=x > 0$

Ta có $\Large V_{S.ABD}=\dfrac{1}{3}S_{ABD}.SA=\dfrac{a^2x}{6}$.

Lại có $\Large \dfrac{V_{S.AHK}}{V_{S.ABD}}=\dfrac{SH}{SB}.\dfrac{SK}{SD}$ $\Large =\left(\dfrac{SA}{SB}\right)^2.\left(\dfrac{SA}{SD}\right)^2=\dfrac{x^4}{(x^2+a^2)^2}$

$\Large \Rightarrow V_{S.AHK}=\dfrac{x^4}{(x^2+a^2)^2}.V_{S.ABD}=\dfrac{a^2x^5}{6(x^2+a^2)^2}$.

Gọi $\Large O=AC\cap BD$, $\Large G=SO\cap HK$, $\Large I=AG\cap SC$.

Ta có $\Large \left\{\begin{align} & BC\perp AB \\ & BC\perp SA \end{align}\right.$ $\Large \Rightarrow BC\perp (SAB) \Rightarrow BC\perp AH$

Lại có $\Large \left\{\begin{align} & AH\perp SB \\ & AH\perp BC \end{align}\right.$ $\Large \Rightarrow AH\perp (SBC) \Rightarrow AH\perp SC$

Chứng minh tương tự ta có $\Large AK \perp SC$

Vì $\Large \left\{\begin{align} & SC\perp AK \\ & SC\perp AH \end{align}\right.$ $\Large \Rightarrow SC\perp (AHK)$ $\Large AI\subset (AHK)$ $\Large \Rightarrow SC\perp AI$.

Xét tam giác $\Large SAC$ vuông tại $\Large A$ và có $\Large AC=a\sqrt{2}$, $\Large AI\perp SC$

$\Large \Rightarrow \dfrac{IC}{IS}=\left(\dfrac{AC}{AS}\right)^2=\dfrac{2a^2}{x^2}$ $\Large \Rightarrow CI=\dfrac{2a^2}{x^2}SI$.

$\Large \Rightarrow V_{ACHK}=\dfrac{1}{3}S_{AHK}.CI$ $\Large =\dfrac{1}{3}S_{AHK}.\dfrac{2a^2}{x^2}.SI$ $\Large =\dfrac{2a^2}{x^2}V_{S.AHK}$ $\Large =\dfrac{a^4}{3}.\dfrac{x^3}{(x^2+a^2)^2}$.

Ta lại có $\Large (x^2+a^2)^2=\left(\dfrac{x^2}{3}+\dfrac{x^2}{3}+\dfrac{x^2}{3}+a^2\right)^2 \overset{AM-GM}{\geq}$ $\Large 16\dfrac{x^3a}{3\sqrt{3}}\Rightarrow \dfrac{x^3}{(x^2+a^2)^2}\leq \dfrac{3\sqrt{3}}{16a}$ (Dấu "=" xảy ra khi và chỉ khi $\Large x=a\sqrt{3}$).

Suy ra $\Large V_{ACHK}\leq \dfrac{a^4}{3}.\dfrac{3\sqrt{3}}{16a}$ $\Large \Leftrightarrow V_{ACHK}\leq \dfrac{a^3\sqrt{3}}{16}$.

Vậy giá trị lớn nhất của thể tích khối tứ diện $\Large ACHK$ bằng $\Large \dfrac{a^3\sqrt{3}}{16}$ khi $\Large x=SA=a\sqrt{3}$.