Cho phương trình $\Large 3^x(3^{2x}+1)-(3^x+m+2)\sqrt{3^x+m+3}=2\sqrt{

Cho phương trình $\Large 3^x(3^{2x}+1)-(3^x+m+2)\sqrt{3^x+m+3}=2\sqrt{3^x+m+3}$, với $\Large m$ là tham số. Có bao nhiêu giá trị nguyên âm của $\Large m$ để phương trình có nghiệm thực?

• A. 3.
• B. 6.
• C. 4.
• D. 5.

$\Large 3^x(3^{2x}+1)-(3^x+m+2)\sqrt{3^x+m+3}=2\sqrt{3^x+m+3}$

$\Large \Leftrightarrow 3^x(3^{2x}+1)=(3^x+m+2)\sqrt{3^x+m+3}+2\sqrt{3^x+m+3}$

$\Large \Leftrightarrow 3^{3x}+3^x=(3^x+m+3)\sqrt{3^x+m+3}+\sqrt{3^x+m+3}$

$\Large \Leftrightarrow 3^{3x}+3^x=\left(\sqrt{3^x+m+3}\right)^3+\sqrt{3^x+m+3}$ (1)

Xét hàm đặc trưng $\Large f(t)=t^3+t$ có $\Large {f}'(t)=3t^2+1 > 0, \forall t\in\mathbb{R}$.

Vậy 

(1) $\Large \Leftrightarrow 3^{3x}+3^x=\left(\sqrt{3^x+m+3}\right)^3+\sqrt{3^x+m+3}$

$\Large \Leftrightarrow f(3^x)=f\left(\sqrt{3^x+m+3}\right)$

$\Large \Leftrightarrow 3^x=\sqrt{3^x+m+3}$

$\Large \Leftrightarrow 3^{2x}-3^x-3=m$.

Đặt $\Large u=3^x$ với điều kiện $\Large u > 0$ và đặt $\Large g(u)=u^2-u-3$. Phương trình (*) $\Large \Leftrightarrow g(u)=m$.

Mà $\Large {g}'(u)=2u-1$, $\Large {g}'(u)=0$ $\Large \Leftrightarrow u=\dfrac{1}{2}$ ta có bảng biến thiên của $\Large g(u)$

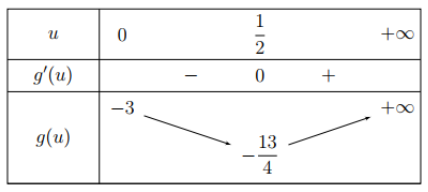
Từ bảng biến thiên ta thấy phương trình đã cho có nghiệm thực khi và chỉ khi $\Large m > -\dfrac{13}{4}$.

Vậy có tất cả 3 giá trị nguyên âm của $\Large m$ để phương trình có nghiệm thực là $\Large -3; -2; -1$.

Chọn đáp án A