Trong không gian với hệ tọa độ $\Large Oxyz$, cho hai mặt cầu $\Large

Trong không gian với hệ tọa độ $\Large Oxyz$, cho hai mặt cầu $\Large (S_1): (x-2)^2+(y+3)^2+(z-1)^2=4$ và $\Large (S_2): (x-3)^2+(y+1)^2+(z+1)^2=1$. Gọi $\Large M$ là điểm thay đổi thuộc mặt cầu $\Large (S_2)$ sao cho tồn tại ba mặt phẳng đi qua $\Large M$, đôi một vuông góc với nhau và lần lượt cắt mặt cầu $\Large (S_1)$ theo ba đường tròn. Giá trị lớn nhất của tổng chu vi ba đường tròn đó là

• A.

  $\Large 8\pi$.

• B.

  $\Large 4\sqrt{6}\pi$.

• C.

  $\Large 2\sqrt{30}\pi$.

• D.

  $\Large 4\pi$.

$\Large (S_1)$ có tâm $\Large I_1(2; -3; 1)$, bán kính $\Large R_1=2$.

$\Large (S_2)$ có tâm $\Large I_2(3; -1; -1)$, bán kính $\Large R_2=1$.

$\Large I_1I_2=3=R_1+R_2\Rightarrow (S_1)$ tiếp xúc ngoài với $\Large (S_2)$.

Gọi ba mặt phẳng đi qua $\Large M$, đôi một vuông góc với nhau và lần lượt cắt mặt cầu $\Large (S_1)$ là $\Large (P), (Q), (R)$, bán kính các đường tròn giao tuyến lần lượt là $\Large r_1, r_2, r_3$.

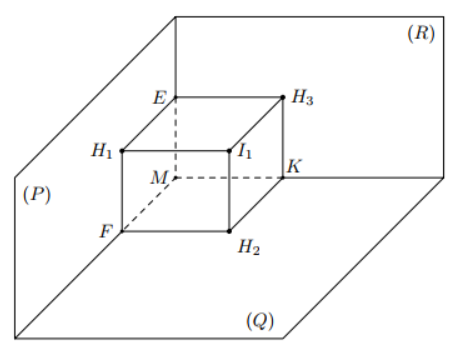
Gọi hình chiếu của $\Large I_1$ lên $\Large (P), (Q), (R)$ lần lượt là $\Large H_1, H_2, H_3$,

Dựng hình hộp chữ nhật $\Large EH_3I_1H_1.MKH_2F$.

Xét hình hộp chữ nhật $\Large EH_3I_1H_1.MKH_2F$ có

$\Large I_1H_1^2+I_1H_2^2+I_1H_3^2=I_1M^2$ $\Large \Leftrightarrow 4-r_1^2+4-r_2^2+4-r_3^2=I_1M^2$ $\Large \Leftrightarrow r_1^2+r_2^2+r_3^2=12-I_1M^2$.

Tổng chu vi của ba đường tròn là

$\Large 2\pi (r_1+r_2+r_3)\leq 2\pi\sqrt{3(r_1^2+r_2^2+r_3^2)}$ $\Large =2\pi\sqrt{3(12-I_1M^2)}\leq 2\pi\sqrt{3(12-R_1^2)}=2\pi\sqrt{3(12-4)}=4\sqrt{6}\pi$.

Dấu "=" xảy ra $\Large \Leftrightarrow M$ là điểm tiếp xúc của $\Large (S_1)$ và $\Large (S_1)$.

Chọn đáp án B