Cho hàm số bậc ba $\Large y=f(x)=ax^3-\dfrac{1}{2}x^2+cx+d$ và parabol

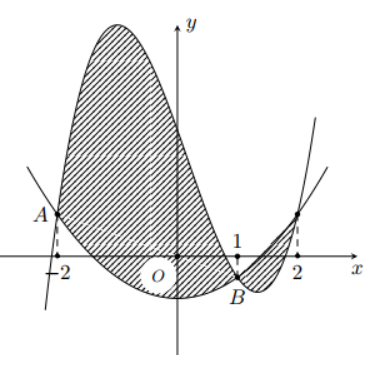
Cho hàm số bậc ba $\Large y=f(x)=ax^3-\dfrac{1}{2}x^2+cx+d$ và parabol $\Large y=g(x)$ có đồ thị như hình vẽ

Biết $\Large AB=\dfrac{3\sqrt{5}}{2}$, diện tích hình phẳng giới hạn bởi hai đồ thị $\Large y=f(x)$ và $\Large y=g(x)$ bằng

• A. $\Large \dfrac{71}{12}$
• B. $\Large \dfrac{71}{6}$
• C. $\Large \dfrac{45}{4}$
• D. $\Large \dfrac{93}{9}$

Parabol $\Large y=g(x)$ có dạng: $\Large y=kx^2+m$, $\Large (k, m\in \mathbb{R}, k > 0)$.

Suy ra tọa độ các điểm $\Large A(-2; 4k+m); B(1; k+m)$.

Lại có $\Large AB=\dfrac{3\sqrt{5}}{2}\Leftrightarrow \sqrt{9+9k^2}=\dfrac{3\sqrt{5}}{2}$ $\Large \Leftrightarrow 1+k^2=\dfrac{5}{4}\Leftrightarrow k=\dfrac{1}{2}$ (loại nghiệm $\Large k=-\dfrac{1}{2}$).

Do đó $\Large y=g(x)=\dfrac{1}{2}x^2+m$.

Mặt khác, phương trình hoành độ giao điểm của hai đồ thị hàm số $\Large f(x)$ và $\Large g(x)$ là $\Large f(x)-g(x)=0$ $\Large \Leftrightarrow ax^3-x^2+cx+(d-m)=0$.

Vì hai đồ thị cắt nhau tại 3 điểm có hoành độ lần lượt là $\Large -2, 1, 2$ nên 

$\Large ax^3-x^2+cx+(d-m)=a(x+2)(x-1)(x-2)\ \forall x\in\mathbb{R}$

$\Large \Leftrightarrow ax^3-x^2+cx+(d-m)=a(x^3-x^2-4x+4)\ \forall x\in\mathbb{R}$.

Đến đây ta tìm $\Large a$ bằng cách đồng nhất hệ số của $\Large x^2$ ở hai vế.

Từ đó ta có $\Large -1=-a\Leftrightarrow a=1$.

Diện tích hình phẳng giới hạn bởi hai đồ thị là

$\Large S=\int\limits_{-2}^2\left|(x+2)(x-1)(x-2)\right|\text{d}x=\dfrac{71}{6}$.

Chọn đáp án B