Cho hình chóp S.ABC có SA vuông góc với đáy, đáy là tam giác đều, $\La

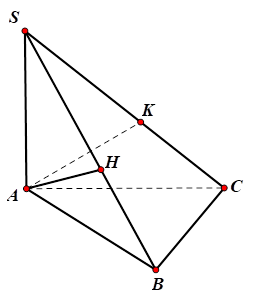
Cho hình chóp S.ABC có SA vuông góc với đáy, đáy là tam giác đều, $\Large SA=a\sqrt{3}$ và góc giữa đường thẳng SB và đáy bằng $\Large 60^{\circ}.$ Gọi H, K lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính bán kính mặt cầu đi qua các điểm A, B, H, K.

• A.

  $\Large \dfrac{a}{2}.$

• B.

  $\Large \dfrac{\sqrt{3}a}{6}.$

• C.

  $\Large \dfrac{a\sqrt{3}}{2}.$

• D.

  $\Large \dfrac{\sqrt{3}a}{3}.$

Chọn D

Cách 1:

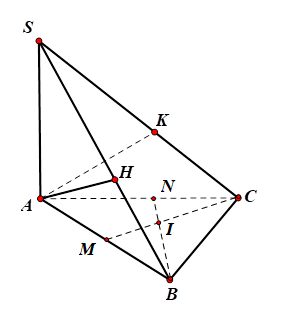
Góc giữa đường thẳng SB và đáy bằng $\Large 60^{\circ} $$\Large \Rightarrow \widehat {SAB} = 60^\circ  \Rightarrow AB=\dfrac{SA}{\tan 60^{\circ}}=\dfrac{a\sqrt{3}}{\sqrt{3}}=a.$

Gọi BN, CM lần lượt là hai đường cao của tam giác ABC và I là trọng tâm của $\Large \Delta ABC.$

Do tam giác ABC đều nên M, N lần lượt là trung điểm của các cạnh AB, AC.

Tam giác ABH vuông tại H nên M là tâm đường tròn ngoại tiếp tam giác ABH, mặt khác $\Large \left\{\begin{align} & CM \perp AB \\ & CM \perp SA \end{align}\right.$ $\Large \Rightarrow CM \perp (SAB),$ ta suy ra CM là trục của đường tròn ngoại tiếp tam giác ABH. Hoàn toàn tương tự ta có BN là trục của đường tròn ngoại tiếp tam giác ACK. Từ đó suy ra $\Large IA=IB=IH=IC=IK$ hay I là tâm mặt cầu đi qua các điểm A, B, H, K bán kính mặt cầu là $\Large R=IA=\dfrac{2}{3}.\dfrac{AB\sqrt{3}}{2}=\dfrac{AB\sqrt{3}}{3}.$

Vậy $\Large R=\dfrac{AB\sqrt{3}}{3}=\dfrac{a\sqrt{3}}{3}.$

Cách 2:

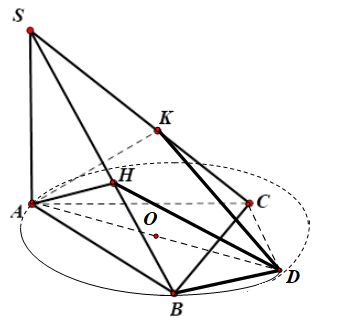
Gọi O là tâm đường tròn ngoại tiếp $\Large \Delta ABC$ và D là điểm đối xứng của A qua điểm O.

Ta có $\Large BD \perp AB$ và $\Large BD\perp SA \Rightarrow BD \perp (SAB) \Rightarrow BD \perp AH.$

Từ giả thuyết $\Large \Rightarrow AH \perp SB$

$\Large \Rightarrow AH\perp (SBD) \Rightarrow AH \perp HD.$

Tương tự $\Large AK \perp KD.$

Do các điểm B, H, K nhìn AD dưới một góc vuông nên B, H, K nằm trên mặt cầu đường kính AD.

$\Large \left( {SB;(ABC)} \right) = \widehat {SBA} = 60^\circ $

$\Large \tan \widehat {SBA}=\dfrac{SA}{AB} \Rightarrow AB=\dfrac{SA}{\tan 60^{\circ}}=a.$ Tam giác ABC đều cạnh a ta có $\Large AO=\dfrac{a\sqrt{3}}{3}.$

Vậy mặt cầu qua A, B, H, K có bán kính $\Large R=\dfrac{AD}{2}=AO=\dfrac{a\sqrt{3}}{3}.$