Cho một tấm tôn hình tròn có diện tích $\large 4 \pi \mathrm{dm}^{2}$.

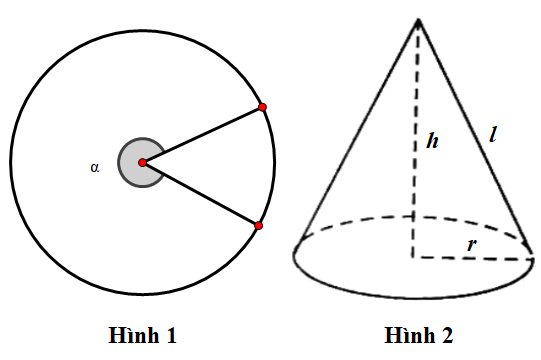
Cho một tấm tôn hình tròn có diện tích $\large 4 \pi \mathrm{dm}^{2}$. Người ta cắt thành một hình quạt có góc ở đỉnh là $\large \alpha(0<\alpha<2 \pi)$ như hình 1 để làm thành cái gầu múc nước hình nón như hình 2. Thể tích lớn nhất của cái gầu là:

• A.

  A. $\large \dfrac{16 \sqrt{3} \pi}{27}\left(\mathrm{dm}^{3}\right)$

• B.

  B. $\large \dfrac{\pi \sqrt{3}}{3}\left(\mathrm{dm}^{3}\right)$

• C.

  C. $\large \dfrac{3 \sqrt{7} \pi}{9}\left(\mathrm{dm}^{3}\right)$

• D.

  D. $\large \dfrac{2 \sqrt{2} \pi}{3}\left(\mathrm{dm}^{3}\right)$

Ta có đường sinh l của hình nón là bán kính R=2dm của hình tròn

Bán kính đáy của hình nón: $\large r=\dfrac{2 \alpha}{2 \pi}=\dfrac{\alpha}{\pi}$

Đường cao của hình nón: $\large h=\sqrt{2^{2}-\dfrac{\alpha^{2}}{\pi^{2}}}=\dfrac{1}{\pi} \cdot \sqrt{4 \pi^{2}-\alpha^{2}}(0<\alpha<2\pi)$

Khi đó thể tích hình nón: $\large V(\alpha)=\dfrac{1}{3\pi^2}.\alpha^2.\sqrt{4\pi^2-\alpha^2}. \\ \text{Suy ra: }\mathrm{V'}(\alpha)=\dfrac{1}{3 \pi^{2}}.\left(2 \alpha \sqrt{4 \pi^{2}-\alpha^{2}}-\dfrac{\alpha^{3}}{\sqrt{4 \pi^{2}-\alpha^{2}}}\right)=\dfrac{1}{3 \pi^{2}} \cdot\alpha\cdot\left(\dfrac{-3 \alpha^{2}+8 \alpha \pi^{2}}{\sqrt{4 \pi^{2}-\alpha^{2}}}\right)$

$\large \mathrm{V}^{\prime}(\alpha)=0 \Leftrightarrow\left[\begin{array}{l}
\alpha=0 \notin(0 ; 2 \pi) \\
\alpha=\dfrac{2 \sqrt{6} \pi}{3} \in(0;2\pi) \\
\alpha = \dfrac{-2 \sqrt{6} \pi}{3} \notin(0 ; 2 \pi)
\end{array}\right.$

Với $\Large \alpha=\dfrac{2 \sqrt{6} \pi}{3} \Rightarrow \mathrm{V}=\dfrac{1}{3 \pi^{2}} \cdot \dfrac{8}{3} \pi^{2} \cdot \dfrac{2 \sqrt{3} \pi}{3}=\dfrac{16 \sqrt{3} \pi}{27}\left(\mathrm{dm}^{3}\right)$

Bảng biến thiên:

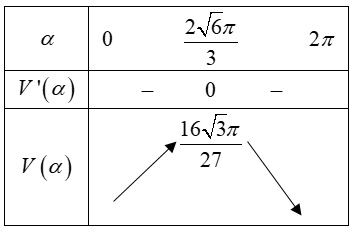
Dựa vào bảng biến thiên suy ra thể tích lớn nhất của cái gầu là: $\Large V=\dfrac{16 \sqrt{3} \pi}{27}{dm}^{3}$