Cho hình chóp $\Large S.ABCD$ có đáy là hình thang vuông tại $\Large A

Cho hình chóp $\Large S.ABCD$ có đáy là hình thang vuông tại $\Large A$ và $\Large D$, $\Large AB = 2a$, $\Large AD = CD = a$, $\Large SA$ vuông góc với mặt phẳng đáy và $\Large SA = a \sqrt{6}$ (minh họa như hình vẽ). Góc giữa đường thẳng $\Large SC$ và mặt phẳng $\Large (ABCD)$ bằng

• A.

  A. $\Large 60^{\circ}.$

• B.

  B. $\Large 45^{\circ}.$

• C.

  C. $\Large 30^{\circ}.$

• D.

  D. $\Large 90^{\circ}.$

Chọn A

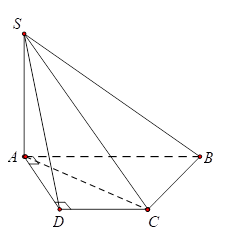
Theo giả thiết $\Large SA \perp (ABCD)$ suy ra $\Large \widehat{(SC, (ABCD))} = \widehat{SCA}.$

Từ giả thiết suy ra tam giác $\Large ACD$ vuông cân tại $\Large D$ nên $\Large AC = AD \sqrt{2} = a \sqrt{2}.$

Xét tam giác $\Large SAC$ vuông tại $\Large A$ ta có:

$\Large \tan \widehat{SCA} = \dfrac{SA}{AC} = \dfrac{a\sqrt{6}}{a\sqrt{2}} = \sqrt{3}$, do đó $\Large \widehat{SCA} = 60^{\circ}$.

Vậy góc giữa đường thẳng $\Large SC$ và mặt phẳng $\Large (ABCD)$ bằng $\Large 60^{\circ}$.