Cho ba hàm số $\large y=f(x), y=g(x), y=h(x)$ có đồ thị của các hàm số

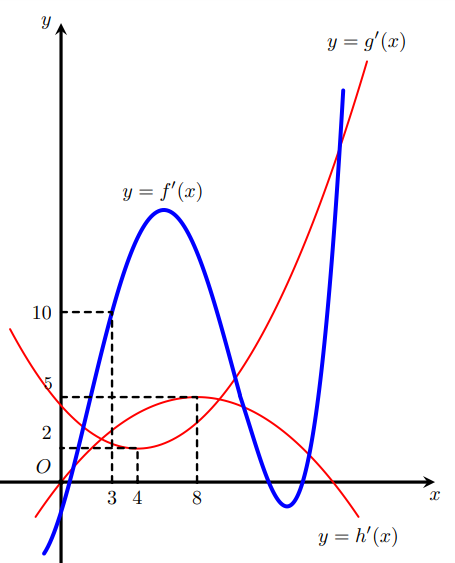
Cho ba hàm số $\large y=f(x), y=g(x), y=h(x)$ có đồ thị của các hàm số $\large y=f^{\prime}(x), y=g^{\prime}(x)$ và $\large y=h^{\prime}(x)$ như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số $\large y=f^{\prime}(x)$. Hàm số $\large k(x)=f(x+7)+g\left(2 x+\dfrac{15}{2}\right)-h\left(4 x+\dfrac{3}{2}\right)$ đồng biến trên khoảng nào dưới đây?

• A.

  A. $\large \left(-\dfrac{17}{4} ; 0\right)$.

• B.

  B. $\large \left(-\infty ; \dfrac{1}{4}\right)$.

• C.

  C. $\large \left(\dfrac{3}{8} ; 1\right)$.

• D.

  D. $\large \left(\dfrac{3}{8} ;+\infty\right)$.

Chọn đáp án C

Ta có $\Large k^{\prime}(x)=f^{\prime}(x+7)+2 g^{\prime}\left(2 x+\dfrac{15}{2}\right)-4 h^{\prime}\left(4 x+\dfrac{3}{2}\right)$

Xét đáp án C

$\Large \dfrac{3}{8}10$

$\Large \dfrac{3}{8}5 \Leftrightarrow 2 g^{\prime}\left(2 x+\dfrac{15}{2}\right)>10$

$\Large \dfrac{3}{8}

Suy ra $\Large k^{\prime}(x)=f^{\prime}(x+7)+2 g^{\prime}\left(2 x+\dfrac{15}{2}\right)-4 h^{\prime}\left(4 x+\dfrac{3}{2}\right)>10+10-20=0$

Vậy hàm số k(x) đồng biến trên $\Large \left(\dfrac{3}{8} ; 1\right)$