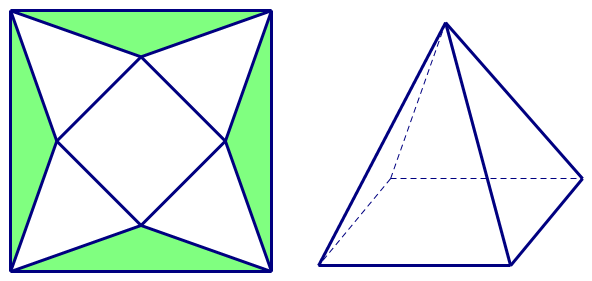
Cho một tấm nhôm hình vuông cạnh 1m như hình vẽ dưới đây. Người ta cắt

Cho một tấm nhôm hình vuông cạnh 1m như hình vẽ dưới đây. Người ta cắt phần tô đậm của nhôm rồi gập lại thành một hình chóp tứ giác đều có cạnh đáy x (cm) sao cho bốn đỉnh của hình vuông gập lại thành đỉnh của hình chóp. Giá trị của x để khối chóp nhận được có thể tích lớn nhất là

• A.

  A. $\large x=\dfrac{1}{2}$

• B.

  B. $\large x=\dfrac{\sqrt{2}}{4}$

• C.

  C. $\large x=\dfrac{\sqrt{2}}{3}$

• D.

  D. $\large x=\dfrac{2 \sqrt{2}}{5}$

Đáp án D

Ta có hình vẽ

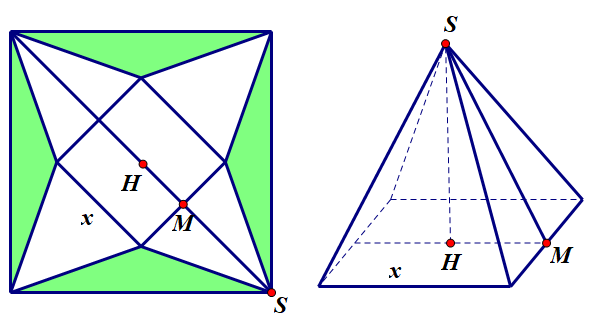
Kí hiệu như hình vẽ. Do hình vuông có cạnh là 1m nên độ dài đường chéo của hình vuông là $\large \sqrt{2} m$. Lúc này ta có $\large M S=\dfrac{\sqrt{2}-x}{2} \mathrm{m}$.

Vậy áp dụng định lý pytago cho tam giác vuông SHM ta có:

$\large S H=\sqrt{S M^{2}-H M^{2}}=\sqrt{\left(\dfrac{\sqrt{2}-x}{2}\right)^{2}-\left(\dfrac{x}{2}\right)^{2}}=\dfrac{1}{2} \cdot \sqrt{2-2 \sqrt{2} x}$

Vậy $\large V=\dfrac{1}{3} \cdot S H. x^{2}=\dfrac{1}{3} \cdot \dfrac{1}{2} \cdot \sqrt{2-2 \sqrt{2} x} .x^{2}$

Xét hàm số $\Large f(x)=\dfrac{1}{3} \cdot \dfrac{1}{2} \cdot \sqrt{2-2 \sqrt{2} x} .x^{2}$

Điều kiện $\large 0

Ta có: $\Large f'(x)=2x \sqrt{2-2 \sqrt{2} x}-\dfrac{x^2.2 \sqrt{2}}{\sqrt{2-2 \sqrt{2} x}}$

$\large f^{\prime}(x)=0 \Leftrightarrow 2 \sqrt{2-2 \sqrt{2} x}-\dfrac{x \sqrt{2}}{\sqrt{2-2 \sqrt{2} x}}=0$

$\large \Leftrightarrow 2(2-2 \sqrt{2} x)=x \sqrt{2} \Leftrightarrow x=\dfrac{4}{5 \sqrt{2}}=\dfrac{2 \sqrt{2}}{5}\in(0;\dfrac{\sqrt{2}}{2})$

Lập bảng biến thiên ta suy ra khối chóp có thể tích lớn nhất khi  $\Large x=\dfrac{2 \sqrt{2}}{5}$