Cho một hình cầu nội tiếp hình nón tròn xoay có góc ở đỉnh là $\large

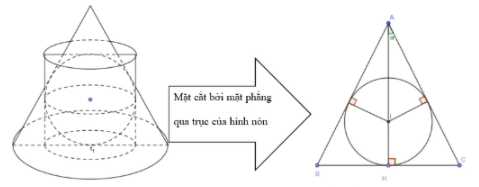
Cho một hình cầu nội tiếp hình nón tròn xoay có góc ở đỉnh là $\large 2\alpha$, bán kính đáy là R và chiều cao là h. Một hình trụ ngoại tiếp hình cầu đó có đáy dưới nằm trong mặt phẳng đáy của hình nón (tham khảo hình vẽ). Gọi $\large V_{1},V_{2}$ lần lượt là thể tích của hình nón và hình trụ biết rằng $\large V_{1}\neq V_{2}$. Gọi M là giá trị lớn nhất của tỉ số $\large \dfrac{V_{2}}{V_{1}}$. Giá trị của biểu thức P = 48M + 25 thuộc khoảng nào dưới đây?

• A. A. (40;60)
• B. B. (60;80)
• C. C. (20;40)
• D. D. (0;20)

Chọn B

Gọi r là bán kính hình cầu, khi đó r cũng là bán kính đường tròn đáy của hình trụ đã cho, chiều cao của hình trụ bằng 2r.

$\large \left\{\begin{matrix}
V_{1} = \dfrac{1}{3}\pi R^{2}h & \\ 
V_{2} = \pi r^{2}.2r & 
\end{matrix}\right.\Rightarrow \dfrac{V_{2}}{V_{1}} = \dfrac{6r^{3}}{R^{2}h}$ 

Xét mặt cắt qua trục của hình nón là 1 tam giác cân ABC có diện tích là $\large S = \dfrac{1}{2}h.2R = Rh$ 

Tam giác cân có chiều dài cạnh bên $\large AB = AC = \dfrac{R}{sin\alpha }$ 

Mặt khác áp dụng công thức S = pr với p là nửa chu vi tam giác,r là bán kính đường tròn nội tiếp tam giác (cũng là bán kính mặt cầu đã cho).

Ta có:

$\large p = \dfrac{1}{2}\left (2R+2\dfrac{R}{sin\alpha }  \right ) \Rightarrow S = Rh = \left (R+\dfrac{R}{sin\alpha }  \right )r \Leftrightarrow r = \dfrac{h.sin\alpha }{sin\alpha +1}$ 

Khi đó $\large \dfrac{V_{2}}{V_{1}} = \dfrac{6h^{3}sin^{3}\alpha }{R^{2}h(sin\alpha +1)^{3}} = \dfrac{6sin^{3}\alpha }{(sin\alpha +1)^{3}}.\left (\dfrac{h}{R}  \right )^{2}$ 

$\large = \dfrac{6sin^{3}\alpha }{(sin\alpha +1)^{3}}.cot^{2}\alpha = \dfrac{6sin\alpha (1-sin^{2}\alpha )}{(sin\alpha +1)^{3}} = \dfrac{6sin\alpha (1-sin\alpha )}{(sin\alpha +1)^{2}}$ 

Xét hàm số $\large y = \dfrac{6sin\alpha (1-sin\alpha )}{(sin\alpha +1)^{2}}$ 

Đặt $\large t = sin\alpha , t \in (0;1)$ ta có $\large y = \dfrac{6t(1-t)}{(t +1)^{2}}, t \in (0;1)$.

Ta có $\large y’ = \dfrac{-6(3t-1)}{(t+1)^{3}}; y' = 0 \Rightarrow t = \dfrac{1}{3}$ 

Bảng biến thiên:

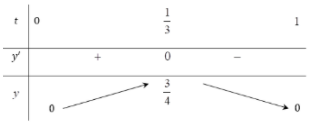
Suy ra $\large M = \dfrac{3}{4}$. Vậy P = 48M+25 = 48.\dfrac{3}{4}+25 = 61$