Cho miếng bìa hình chữ nhật ABCD có AB = 6, AD = 9. Trên cạnh AD lấy đ

Cho miếng bìa hình chữ nhật ABCD có AB = 6, AD = 9. Trên cạnh AD lấy điểm E sao cho AE = 3.Gọi F là trung điểm của BC . Cuốn miếng bìa sao cho AB trùng CD để tạo thành một hình trụ. Tính thể tích của tứ diện ABEF .

• A. $\large \dfrac{81\sqrt{3}}{8\pi^2}$
• B. $\large \dfrac{81\sqrt{3}}{4\pi^2}$
• C. $\large \dfrac{81\sqrt{3}}{4\pi}$
• D. $\large \dfrac{\sqrt{3}}{4\pi^2}$

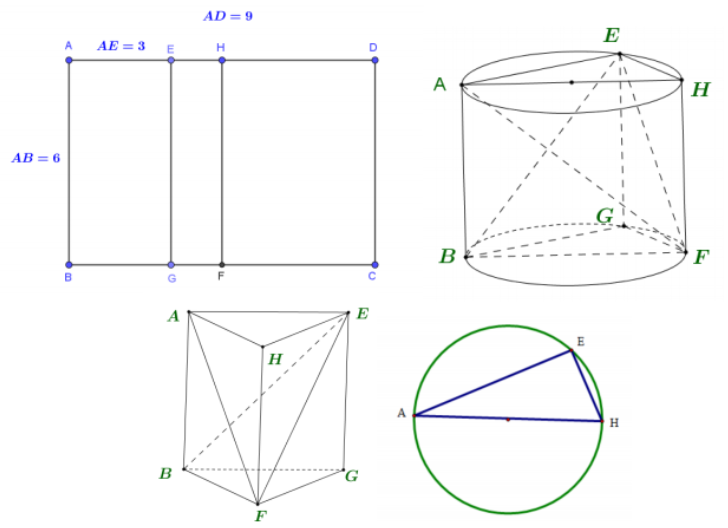
Khi cuốn miếng bìa sao cho AB trùng CD để tạo thành một hình trụ thì chu vi đáy của hình trụ là 9, bán kính đáy là $\large R=\dfrac{9}{2\pi}$ và chiều cao của hình trụ là AB = 6

Gọi G là hình chiếu của E lên đáy dưới của hình trụ, H là hình chiếu của F lên đáy trên của hình trụ. Ta có AH là đường kính của hình trụ suy ra tam giác AHE vuông tại E có $\large \widehat{AHE}=60^\circ, HE=\dfrac{1}{2}AH=R=\dfrac{9}{2\pi}$

Diện tích tam giác AHE là: $\large S=\dfrac{1}{2}AH.HE.\sin 60^\circ=\dfrac{81\sqrt{3}}{8\pi^2}$

Thể tích khối lăng trụ đứng AEH. BGF: $\large V=\dfrac{6.81.\sqrt{3}}{8\pi^2}=\dfrac{243\sqrt{3}}{4\pi^2}$

Thể tích khối tứ diện ABEF bằng thể tích khối tứ diện GBEF và bằng $\large \dfrac{1}{3}V=\dfrac{81\sqrt{3}}{4\pi^2}$

Vậy thể tích của tứ diện ABEF là $\large \dfrac{81\sqrt{3}}{4\pi^2}$