Trong không gian với hệ tọa độ Oxyz , cho mặt cầu $\large (S): (x-1)^2

Trong không gian với hệ tọa độ Oxyz , cho mặt cầu

$\large (S): (x-1)^2+(y-2)^2+(z+1)^2=49$ và mặt phẳng

$\large (\alpha): -2mx+(3-2m)y+(2m-1)z+2m-2=0$ (m là tham số). Mặt phẳng $\large (\alpha)$ cắt (S) theo một đường tròn có diện tích nhỏ nhất là

• A. $\large \dfrac{8974}{96}\pi$
• B. $\large \dfrac{3\sqrt{5}}{\sqrt{14}}\pi$
• C. $\large \dfrac{3\sqrt{5}}{\sqrt{14}}$
• D. Đáp án khác.

+ Mặt cầu (S) có tâm I (1;2;-1) và bán kính R = 7 .
+ Mặt phẳng $\large (\alpha)$ cắt (S) theo một đường tròn (C) có tâm H , bán kính r , diện tích S .
+ Gọi d là khoảng cách từ tâm I đến mặt phẳng $\large (\alpha)$

Ta có: $\large S=\pi r^2=\pi(R^2-d^2)$ suy ra đường tròn (C) có diện tích nhỏ nhất khi và chỉ khi $\large d^2$ lớn nhất.

+ Ta có: $\large d^2=\dfrac{[-2m+(3-2m)2+(2m-1)(-1)+2m-2]^2}{(-2m)^2+(3-2m)^2+(2m-1)^2}=\dfrac{36m^2-60m+25}{12m^2-16m+10}$

+ Xét hàm số: $\large f(m)=\dfrac{36m^2-60m+25}{12m^2-16m+10}, m\in\mathbb{R}$

$\large * f'(m)=\dfrac{144m^2+120m-200}{(12m^2-16m+10)^2}$

$\large f'(m)=0\Leftrightarrow 144m^2+120m-200=0\Leftrightarrow$ $\large \left[\begin{align}& m=\dfrac{5}{6}\\& m=-\dfrac{5}{3}\\\end{align}\right.$

* Bảng biến thiên:

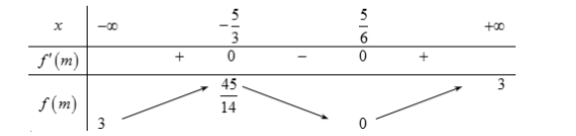
+ $\large d^2$ đạt giá trị lớn nhất khi và chỉ khi f(m) đạt giá trị lớn nhất.
Từ bảng biến thiên của hàm số  y= f(m) suy ra $\large \underset{R}{\max}f(m)=\dfrac{45}{14}$ khi $\large m=-\dfrac{5}{3}$ hay $\large \max d^2=\dfrac{45}{14}\Rightarrow S=\pi (R^2-d^2)=\dfrac{641}{14}\pi$

Vậy diện tích nhỏ nhất của đường tròn là: $\large \dfrac{641}{14}\pi$